4.4 A2FC con el programa SPSS

  • El análisis de los modelos factoriales con el programa SPSS se hace a partir de la opción de los modelos lineales generalizados (Analizar + Modelo lineal general + Univariante).
Modelo lineal generalizado en SPSS

Figura 4.14: Modelo lineal generalizado en SPSS

Cuando se utiliza este procedimiento aparece una ventana en la que se introduce la VD y las VVII. El procedimiento es semejante al estudiado en el tema 2. La diferencia es que aquí introducimos dos o más variables en el cuadro de factores fijos. Asimismo, aparecen una serie de botones que permiten realizar las mismas comparaciones a posteriori que las realizadas en el tema 2. El botón de gráficos permite representar las medias de las distintas condiciones. Con el botón de guardar podemos almacenar las puntuaciones predichas, los errores, valores para el diagnóstico de los supuestos de la prueba. Por último, en el botón de opciones pueden obtenerse resúmenes estadísticos de las variables, pruebas de homogeneidad, estimaciones del tamaño del efecto y de la potencia entre otras posibilidades.

Ventana para introducir las variables

Figura 4.15: Ventana para introducir las variables

Los resultados obtenidos permiten contrastar la hipótesis del diseño (en este caso corresponden a los del ejemplo 1):

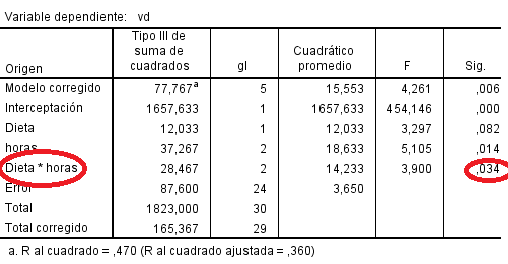
Resultados del ANOVA factorial

Figura 4.16: Resultados del ANOVA factorial

  • En el caso de que la interacción sea significativa es conveniente crear una nueva variable (denominada ab en la siguiente figura), para estudiar el efecto de la interacción:
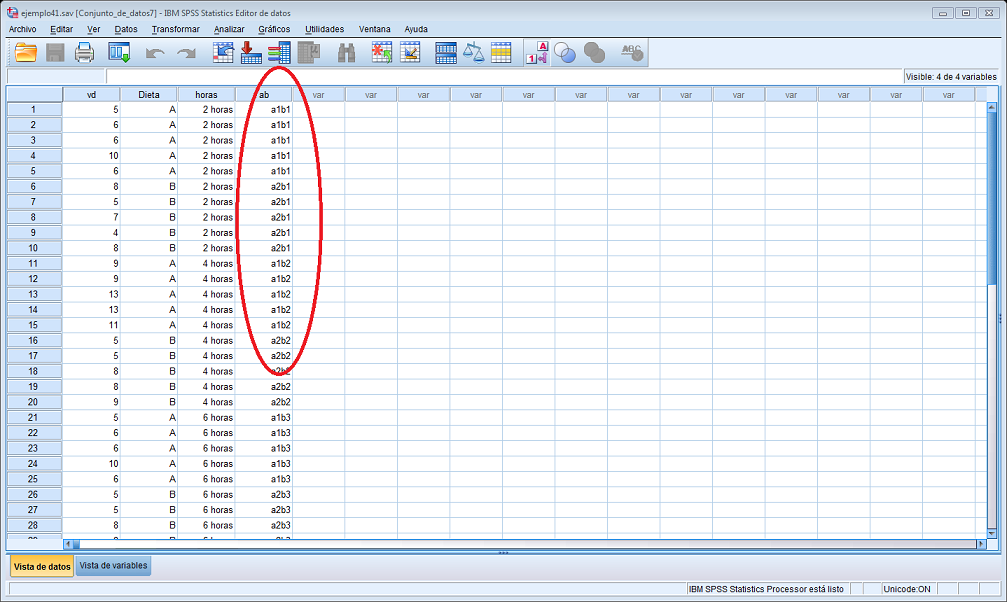
Creación de la variable ab

Figura 4.17: Creación de la variable ab

  • Una vez creada la variable utilizamos el procedimiento de comparar medias estudiado en el tema 2 (Analizar + Comparar medias + ANOVA de 1 factor:
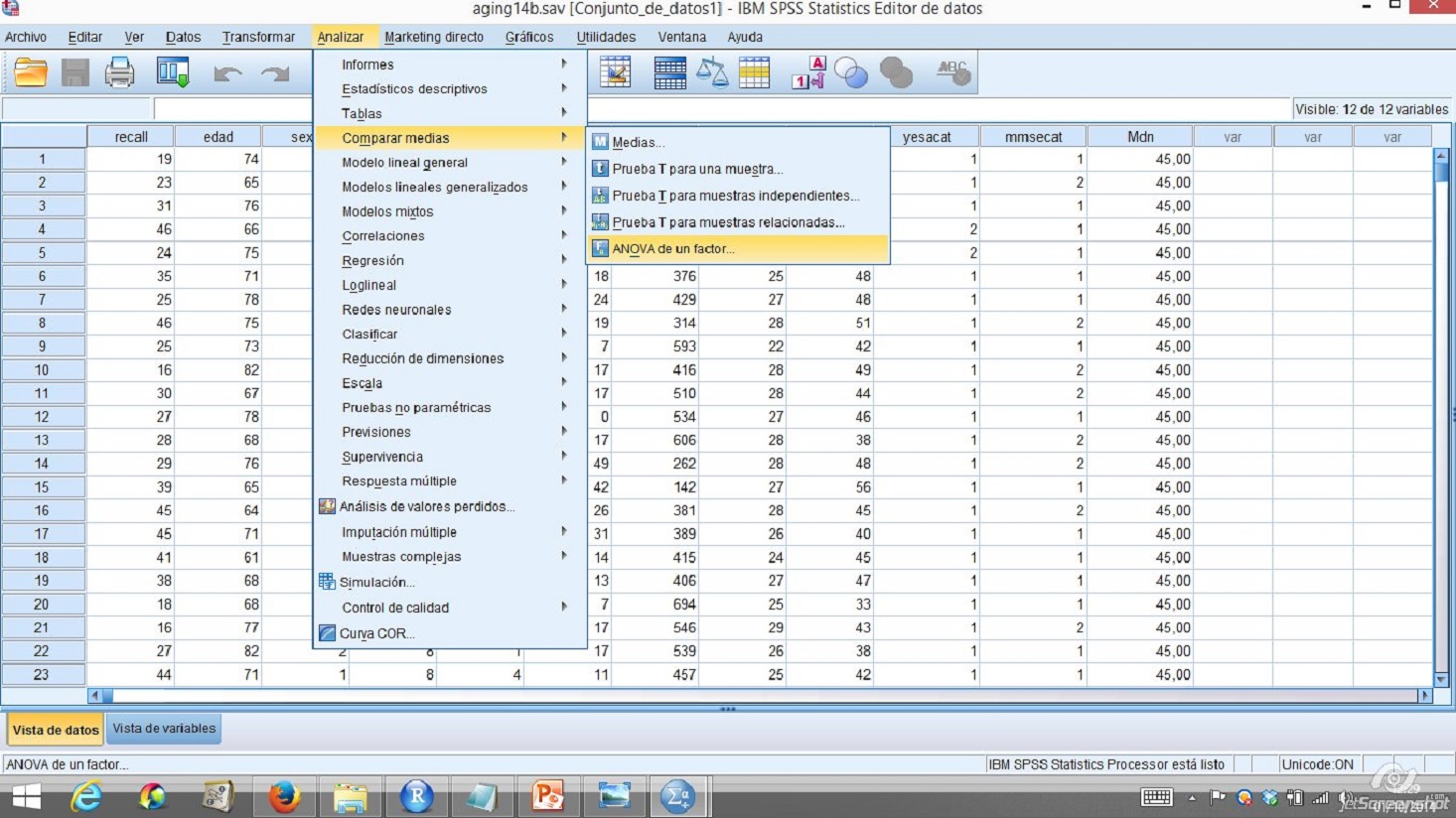
Ventana para seleccionar la opción de modelo lineal

Figura 4.18: Ventana para seleccionar la opción de modelo lineal

  • El paso siguente consiste en introducir la variable dependiente de nuestro diseño (vd en el ejemplo 4.1) en el cuadro denominado Lista de dependientes y la variable ab. En esta ventana pulsaremos el botón de Contrastes para introducir las comparaciones de los efectos simples.
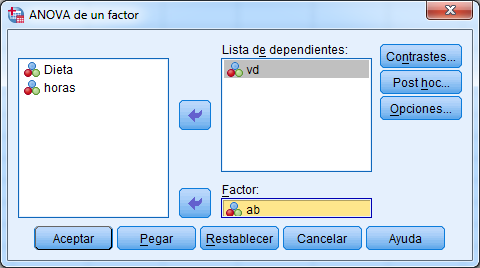
Introducción de las variables

Figura 4.19: Introducción de las variables

  • Para introducir los coeficientes de los contrastes es necesario seguir el orden de las condiciones que aparecen en el fichero de datos. En nuestro caso, el orden es el siguiente para realizar la primera comparación (\(\phi_1\)):
\(\mu_{a_1b_1}\) \(\mu_{a_2b_1}\) \(\mu_{a_1b_2}\) \(\mu_{a_2b_2}\) \(\mu_{a_1b_3}\) \(\mu_{a_2b_3}\)
1 -1 -1 1 0 0
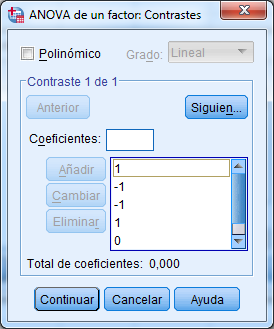
Coeficientes para el primer contraste

Figura 4.20: Coeficientes para el primer contraste

  • Los resultados para este contraste aparecen en la siguiente figura:
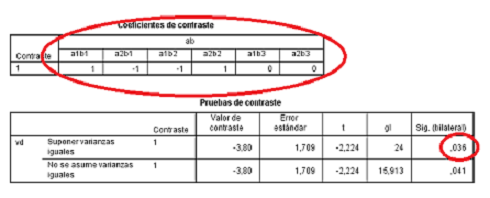
Coeficientes y resultados para el primer contraste

Figura 4.21: Coeficientes y resultados para el primer contraste