6.1 Correlación

En la figura siguiente puede apreciarse visualmente que existe una relación entre la variable edad y la puntuación obtenida en el test de Boston. Se aprecia con cierta claridad que a medida que aumenta la edad disminuye la puntuación obtenida por las personas mayores en el test.

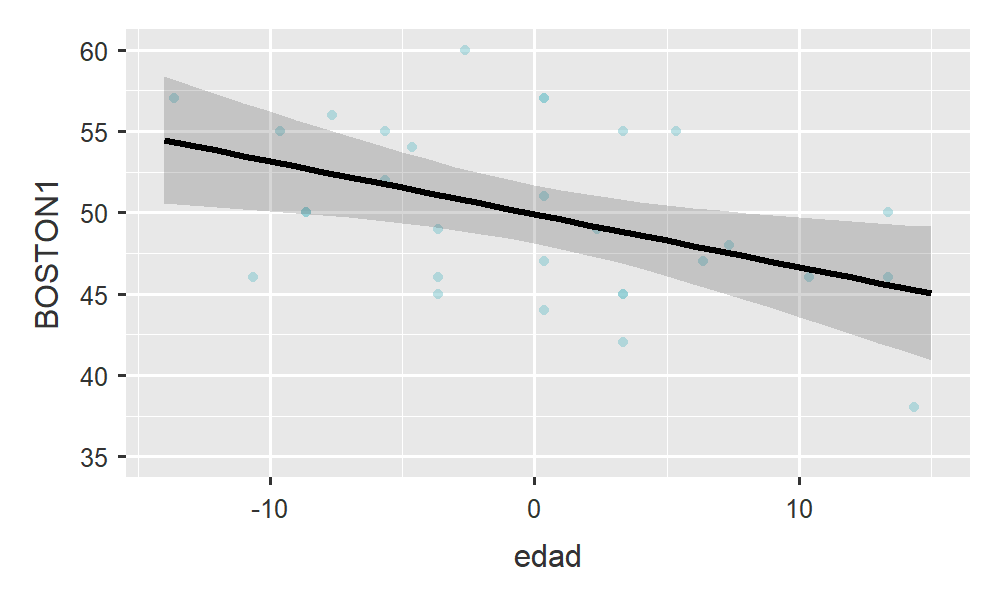
Figura 6.1: Relación entre la edad y BOSTON1

Por lo general, en la investigación científica se desea cuantificar las relaciones entre variables, siendo el coeficiente de correlación de Pearson una de las pruebas más utilizadas. Se define de la siguiente forma:

\[ r_{xy} \approx \frac{\sum_{j=1}^{n}Z_{X_{j}}Z_{Y_{j}}}{n} \] donde \(Z_{X_{j}}\) y \(Z_{Y_{j}}\) son las medidas del sujeto en las variables X e Y expresadas como desviaciones típicas con respecto a su media muestral:

\[ Z_{X_{j}}= \frac{X_{j}-\bar{X}}{SD_{X}} \hspace{10mm} Z_{Y_{j}}= \frac{Y_{j}-\bar{Y}}{SD_{Y}} \]

donde \(SD_{X}\) y \(SD_{Y}\) son la desviación tipo de las variables X e Y respectivamente; \(\bar{X}\) y \(\bar{Y}\) son las medias muestrales.

El coeficiente de correlación (\(r_{xy}\)) oscila entre -1 y 1, siendo su valor cero cuando no existe relación entre las variables. Si la relación es , \(r_{xy}> 0\). Por el contrario, si la relación es \(r_{xy}<0\). Si elevamos al cuadrado \(r_{xy}\) obtenemos el . Nos indica el grado de varianza compartida entre las dos variables. En el caso de la relación entre la variable edad y primera medida del test de Boston el valor sería 0.2158. Es decir, ambas variables comparten el 22% de varianza.

El coeficiente de correlación nos permite conocer el valor de la variable Y a partir de los valores de X. Es decir, si conocemos que una persona está 0,5 desviaciones típicas en edad (es mayor que la media), podremos predecir si esta persona se encuentra por encima o por debajo de la media en la puntuación en el Boston. Para ello, hacemos uso de la siguiente expresión:

\[ \hat{Z}_{Y_{j}}= r_{xy}Z_{X_{j}} = -0.465*0.5 = -0,233 \]

Puede afirmarse que este sujeto se encuentra por debajo del valor medio en la puntuación del test de Boston. De hecho, su edad será:

\[ \hat{Z}_{X_{j}}=0.5 = \frac{X_{j} -67.93}{7.319}= 0.5*7.319 + 67.93 = 71.59 \approx 72 \; años \;de \; edad \] Por tanto, dado que la media de la puntuación en el test de Boston en la primera medición es 49,90 y su desviación tipo es 5,381 podemos hacer una primera estimación del valor que obtendría este sujeto:

\[ \hat{Z}_{Y_{j}}=-0.233 = \frac{Y_{j} -49,90}{5.381}= -2.33*5.381 + 49.40 = 37.346= Y_{j} \]

Este resultado supone una primera aproximación al valor real del sujeto. Podemos considerar que es el valor esperado. Sin embargo, existirán diferencias entre los distintos sujetos que presenten una misma edad. Para determinar el intervalo de confianza será necesario introducirnos en los modelos de regresión.