2.2 ANOVA de 1 factor completamente aleatorizado
Se asume el supuesto de que los distintos grupos representan muestras aleatorias que proceden de poblaciones normales con igual media y varianza y que los errores siguen una distribución normal. La formulación del modelo estadístico es:
\[ Y_{ij} = \mu_{i} + \epsilon_i \]
donde \(Y_{ij}\) es la variable dependiente para el sujeto i del grupo j y \(\mu_{i}\) es el valor esperado (la media). El último elemento del modelo \(\epsilon_{ij}\) es el llamado error o término residual.
Como en todo contraste estadístico, se plantean dos hipótesis, \(H_0\) o hipótesis nula y \(H_1\), hipótesis alternativa. En este modelo se definen de la siguiente forma:
- \(H_{0}\): \(\mu_{1} = \mu_{2} = \cdots \mu_{j}\) (todas las medias son iguales)
- \(H_{1}\): \(\mu_{i} \neq \mu_{j}\) (i \(\neq\) j) (no todas las medias son iguales)
El contraste compara las diferencias entre medias muestrales con la variabilidad experimental para decidir si ésta ha podido generar esas diferencias o no. Tanto la diferencia entre las medias (MCA) como la variabilidad experimental (varianza intrasujeto ó MCE) son dos formas de estimar la varianza poblacional. Bajo el supuesto de hipótesis nula, ambas varianzas deben ser iguales.
La comparación de ambas varianzas sigue una distribución de probabilidad (distribución F) que permite realizar el contraste estadístico:
\[ F = \frac{MC_{A}}{MC_{E}} \sim F(gl_{MC_{A}},gl_{MC_{E}}) \]
Se rechaza \(H_{0}\) si el estadístico F cae dentro de la región crítica; en caso contrario, se mantiene. Si se rechaza esta hipótesis se concluye que no todas las medias son iguales.
Ejemplo 2.1 : A continuación, se presentan los datos de un estudio en el que se quiso comparar los resultados en una prueba de atención de tres grupos de 5 niños (A = sanos, B = con tumor astrocitoma y C = con tumor meduloblastoma)
| A | B | C | |
|---|---|---|---|
| s1 | 30 | 16 | 10 |
| s2 | 35 | 5 | 7 |
| s3 | 15 | 22 | 15 |
| s4 | 21 | 23 | 6 |
| s5 | 24 | 22 | 12 |
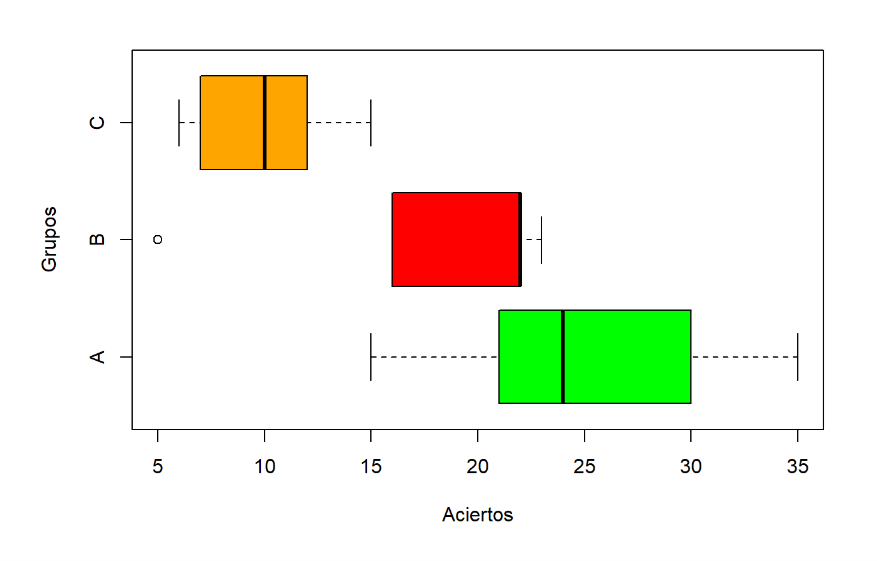
Figura 2.2: Boxplot de los resultados del ejemplo 2.1
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| grupo | 2 | 562.5333 | 281.26667 | 6.426504 | 0.0126711 |
| Residuals | 12 | 525.2000 | 43.76667 | NA | NA |
Los resultados de aplicar el modelo estadístico permiten rechazar la hipótesis nula de que no hay diferencias entre los grupos. Pueden obtenerse los valores de los parámetros que aparecen en el modelo:
\[ Y_{ij} = \mu_{i} + \epsilon_i \]
\(Y_{ij}\) es cada una de las puntuaciones. Así, por ejemplo, \(Y_{1A}\) será el valor del sujeto 1 en el grupo de los sanos \(Y_{1A}\) = 30. Asimismo, \(Y_{1B}\) será la puntuación del primer sujeto del grupo astrocitoma (\(Y_{1B}\) = 16). \(\mu_i\) será la media del grupo. Por tanto, \(\mu_1\) será para el grupo de los individuos sanos 25. Para el grupo astrocitoma será 17.6. Por último, para el grupo meduloblastoma tendremos 10; \(\epsilon_{ij}\) es un valor específico para cada individuo. Es la diferencia entre la puntuación predicha por el modelo y la puntuación obtenida por el individuo. Así, para el sujeto 1 del grupo sano la puntuación predicha será \(Y_{1Apred}\) = 25 y su error \(\epsilon_{ij}\) = 30 - 25 = 5.
Otra forma de plantear este modelo es descomponiendo la puntuación de los sujetos en dos elementos: 1) la variabilidad explicada por el modelo y 2) la variabilidad no explicada por el modelo (error). De este modo, la predicción del modelo (media del grupo) puede descomponerse en dos elementos (media total + diferencia de la media del grupo con respecto a la media total):
\[ Y_{ij} = \mu_{..} + (\mu_j - \mu_{..}) + \epsilon_{ij} \]
donde \(\mu_{..}\) es la media de todas las puntuaciones; \((\mu_j - \mu_{..})\) es la diferencia de la media del grupo y la media total y \(\epsilon_{ij}\) es el error. En el caso de la primera puntuación del grupo sano sería:
30 = 17.5333333 + 7.4666667+ 5