3.2 Ejemplo 1 de diseño unifactorial de medidas repetidas
A continuación, presentamos los resultados de un estudio en el que se quiso estudiar si el contenido emocional de una imagen provocaba cambios en una respuesta psicofisiológica:
| tristeza | neutra | alegria |
|---|---|---|
| 72 | 73 | 80 |
| 64 | 77 | 84 |
| 70 | 83 | 90 |
| 62 | 71 | 86 |
| tristeza | neutra | alegria | |
|---|---|---|---|
| tristeza | 1.00 | 0.37 | -0.20 |
| neutra | 0.37 | 1.00 | 0.67 |
| alegria | -0.20 | 0.67 | 1.00 |
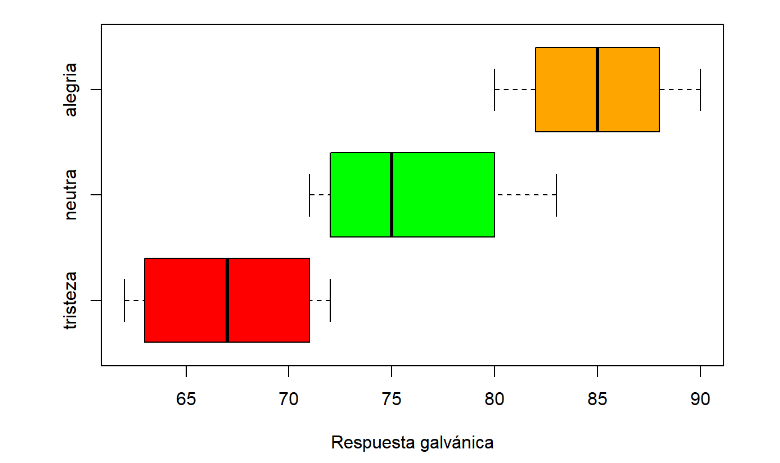
Figura 3.3: Boxplot del ejemplo 3.1
Calculamos las medias cuadráticas del diseño y tenemos:
- Varianza intersujetos:
\[ MC_A = n\sum_{j}(\bar{Y}_{+j}-\bar{Y}_{++})^2/(j-1) = 4((-9)^2 + 0^2 + 9^2)/2 = 648/2 = 324 \]
- Varianza intrasujetos:
\[ MC_S = J\sum_{i}(\bar{Y}_{i+}-\bar{Y}_{++})^2/(n-1) = 3((-1)^2 + (-1)^2 + 5^2 + (-3)^2)/3 = 108/3 = 36 \]
- Varianza del error:
\[ MC_E = \sum_{i}\sum_{j}(Y_{ij}- \bar{Y}_{i+}- \bar{Y}_{+j}-\bar{Y}_{++})^2/[(j-1)(n-1)] = \\ ((72-75-67 + 76)^2 + \cdots + (86-73-85 + 76)^2)/(2*3) = 96/6 = 16 \]
\[ F = \frac{MC_A}{MC_E}= \frac{324}{16}= 20.25 \]
La región crítica en este caso corresponde a \(P(\mathcal{F}_{2,6} > F)\) = 0.002. Por tanto, rechazamos la hipótesis nula de que las medias de las distintas condiciones son iguales. Estos resultados coinciden con los obtenidos mediante el programa R.
## $univariate.tests
## Sum Sq num Df Error SS den Df F value Pr(>F)
## (Intercept) 69312 1 108 3 1925.33 2.606e-05 ***
## emocion 648 2 96 6 20.25 0.002148 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1