6.4 Supuestos del modelo
Una vez obtenido el modelo conviene preguntarse por la idoneidad del mismo. Además del supuesto de linealidad ya mencionado, también es conveniente evaluar la normalidad de los errores y la homogeneidad de las varianzas de la variable Y condicionada a cada valor de X. Asimismo, es conveniente determinar la independencia de las observaciones.
6.4.0.1 Linealidad
El modelo de regresión asume que las relaciones entre las variables son lineales. Sin embargo, no todas las relaciones son de esta naturaleza. Por ejemplo, en la figura 4 podemos observar un tipo de relación curvilínea:

Figura 6.4: Relación entre los años de escolarización y el tiempo en realizar el TMT-B
Cuando se dan este tipo de relaciones no es adecuado aplicar los modelos de regresión aqui estudiados, ya que la interpretación del parámetro \(\beta_{1}\) sería incorrecta (Hayes, 2013). En estas circunstancias han de utilizarse otro tipo de técnicas que superan el alcance de este texto.
6.4.0.2 Normalidad
Este supuesto implica que los errores del modelo siguen una distribución normal. Para evaluar este modelo basta con calcular la diferencia entre las puntuaciones observadas y las predichas (residuales) y aplicar el estadístico de Shapiro-Wilk (SW) para determinar su significación. Aplicado al ejemplo de la figura 1 tenemos:
##
## Shapiro-Wilk normality test
##
## data: mod$residuals
## W = 0.96605, p-value = 0.4376Obsérvese que el test SW no permite rechazar la hipótesis nula de normalidad de la distribución.
6.4.0.3 Homocedasticidad
Este supuesto indica que los errores son homogéneos para cada \(\hat{Y}\). Existen varios métodos para evaluar este supuesto. El más fácil es mediante la evaluación visual de los residuales del modelo representados gráficamente frente a los valores predichos tal y como se realiza en la figura 5. Puede observarse que los errores se reparten de manera homogénea entre los distintos valores predichos.El resultado del incumplimiento de este supuesto implica reducir la potencia estadística de la prueba. Asimismo, los intervalos de confianza se ven afectados por la de los errores.

Figura 6.5: Gráfico para estudiar la homocedasticidad
6.4.0.4 Independencia
Este supuesto implica que la información contenida en los errores de un sujeto no me proporciona información sobre los errores de otros sujetos presentes en el estudio. Por ejemplo, supongamos que estamos interesados en estudiar el rendimiento de los niños en un centro escolar. Obviamente, el rendimiento de los escolares puede depender de la calidad del profesor del que reciben sus enseñanzas. En este caso, todos los alumnos procedentes de un buen profesor presentarán mejores resultados que aquellos que recibieron sus enseñanzas con otro profesor de peor calidad. A la hora de analizar este modelo, los alumnos del profesor “excelente” tenderán a ser positivos en comparación con los de otros niños con peores profesores.
El incumplimiento del supuesto de independencia afecta a los supuestos del modelo de regresión de la misma forma que el supuesto de homocedasticidad. Los errores estándar son infraestimados afectándose también los intervalos de confianza.
6.4.0.5 Colinealidad
Existe colinealidad cuando dos variables predictoras presentan correlaciones my altas. O lo que es lo mismo, existe una relación funcional entre ambas. Si dos variables muestran una colinealidad alta, el procedimiento de estimación de mínimos cuadrados se verá afectado obteniéndose parámetros sesgados (la varianza de los coeficientes de regresión aumentan de manera considerable).
Para detectar la existencia de una colinealidad alta el programa estadístico SPSS muestra dos estadísticos denominados (1 - \(R_{j}^{2}\)) y los (FIV). Este último es el inverso del índice de tolerancia. Valores mayores que 10 en los FIV suelen ir acompañados de los problemas de estimación asociados a un exceso de colinealidad.
Para solucionar los problemas de colinealidad se tienen varias propuestas. Eliminar alguna de las variables que presentan una relación muy alta (esta es la opción que utiliza SPSS cuando se elige la opción de pasos sucesivos). Otra posibilidad es agrupar las distintas variables altamente relacionadas mediante la técnica de . Por último, señalar que cuando se incluyen interacciones entre variables en el modelo es frecuente que aparezcan valores altos de FIV (factores de inflación de la varianza) que pueden solventarse centrando las variables predictoras.
6.4.0.6 Casos atípicos
Para considerar adecuada una recta de regresión, las predicciones deben ser adecuadas. Mediante una primera exploración puede determinarse la existencia de anomalías tanto en la variable dependiente como en las variables predictoras.
Para determinar anomalías en la variable dependiente conviene realizar una exploración de los residuos (\(E_{j}= Y_{j} - \hat{Y}_{j}\)). Por lo general, son aceptables todos aquellos residuos que se encuentren por debajo de 3 (en valor absoluto). Una forma de evaluar que se cumple este supuesto es mediante un gráfico de las puntuaciones predichas y estos residuos. Aplicado al modelo estudiado anteriormente (relación entre edad y medida 1 del Boston) la gráfica es la siguiente:

Figura 6.6: Residuales del modelo
Observamos que todos los residuales se encuentran dentro del rango (-1,2), indicando un buen ajuste del modelo.
Al igual que existen puntuaciones anómalas con respecto a la variable Y, también pueden aparecer puntuaciones atípicas en relación con los valores de los predictores (). Para medir la influencia de este tipo de puntuaciones se calculan los índices \(h_{i}\) que representan el grado de alejamiento del conjunto de puntuaciones de un caso con respecto a las puntuaciones medias de todos los casos. Pardo & San Martin (2011) señalan que una regla que funciona bien es revisar aquellos valores \(h_{i}\) por encima de 0.5.
Una medida basada en los \(h_{i}\) es el estadístico distancias de Cook (\(D_{i}\)) que es la suma de los cambios que se producen en los coeficientes de regresión al ir eliminando cada caso del análisis:
\[ D_{i}=[h_{i}E_{S_{i}^{2}}]/[(p+1)(1-h_{i})] \]
donde \(h_{i}\) es el grado en el que una puntuación es atípica en \(X_{j}\) y \(E_{S_{i}}\) es el grado en que una puntuación es atípica con respecto a Y.
Se considera que un caso debe ser considerado influyente cuando \(D_{i} > 1\). En la siguiente gráfica observamos que las puntuaciones \(D_{i}\) del modelo que relaciona la edad con la medida 1 del Boston se encuentran por debajo de 1:
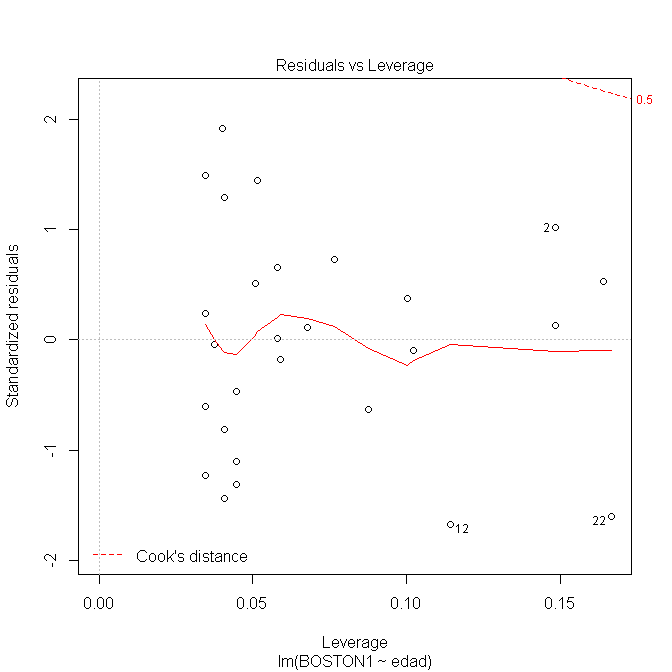
Figura 6.7: Leverage del modelo
6.4.0.7 Interpretación de la regresión múltiple
Para ver como se interpretan los parámetros de un modelo de regresión múltiple vamos a utilizar el ejemplo desarrollado anteriormente en el que se quiso relacionar el efecto el efecto de la educación formal y las actividades estimulantes (AEC) sobre la atención. El modelo a contrastar sería el siguiente:
\[ Atención_{i} = \beta_{0} + \beta_{1}*edad + \beta_{2}*educación + \epsilon_{i} \]
Los resultados que proporciona el programa R son los siguientes:
##
## Call:
## lm(formula = atencion ~ AEC + edu, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -68.157 -7.562 -0.822 9.575 38.855
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -170.1927 19.0477 -8.935 1.50e-09 ***
## AEC 5.1627 0.5497 9.392 5.35e-10 ***
## edu 17.2696 0.9582 18.024 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 24.23 on 27 degrees of freedom
## Multiple R-squared: 0.9549, Adjusted R-squared: 0.9516
## F-statistic: 286.1 on 2 and 27 DF, p-value: < 2.2e-16En base a estos resultados el modelo quedaría explicitado mediante la siguiente ecuación:
\[ Atención_{i} = -170.193 + 5.163*aec + 17.270*educación + \epsilon_{i} \]
Por tanto, las conclusiones siguiendo normas APA serían las siguientes: