6.3 Regresión lineal múltiple
La realidad supone la existencia de relaciones complejas por lo que el investigador suele estar interesado en modelos que incluyan más de dos variables. Para ello, dispone de una serie de herramientas estadísticas dentro de las cuales se incluyen las técnicas de regresión múltiple. El modelo estadístico para esta técnica se representa de la siguiente forma:
\[ Y_{i}= \beta_{0} + \beta_{1}* x_{1i} + \beta_{2}* x_{2i}+ \cdots + \beta_{p+1}* x_{pi}+\epsilon_{i} \]
donde \(x_{pi}\) son las variables predictoras y \(\beta_{p+1}\) son los coeficientes de regresión.
Supongamos que estamos interesados en estudiar si la puntuación en la primera medida del Boston depende de la edad y del género. En la siguiente figura aparece representada la relación entre edad y medida 1 del Boston para hombres y para mujeres:
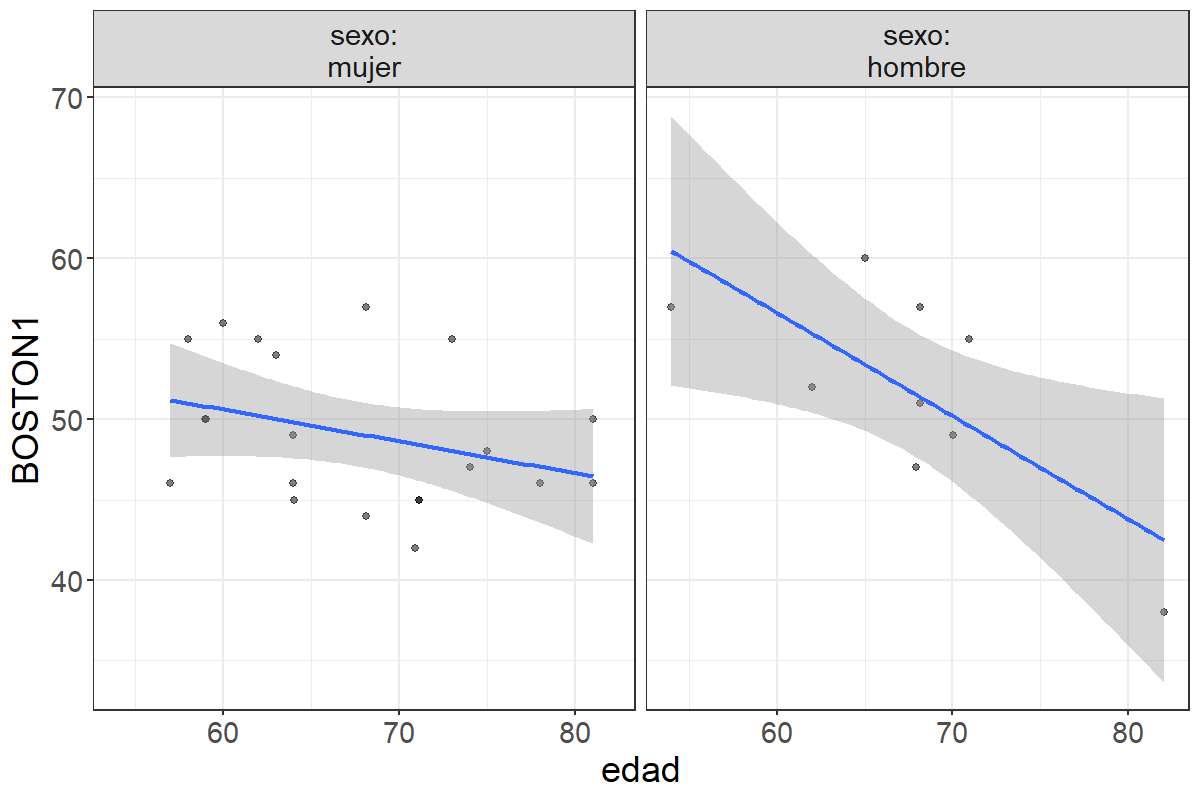
Figura 6.3: Relación entre la edad y el BOSTON1 en función del sexo
La gráfica indica que la relación entre edad y puntuación en el Boston sigue siendo negativa. Sin embargo, esta relación presenta mayor o menor intensidad dependiendo del género. En las mujeres la recta de regresión está menos inclinada indicando que la disminución en la puntuación en el Boston es bastante más atenuada que en los hombres. Realizando el análisis de regresión obtenemos los siguientes resultados:
##
## Call:
## lm(formula = BOSTON1 ~ edad + sexo, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.0949 -3.0146 -0.3378 3.8987 8.0128
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 71.0326 8.0959 8.774 2.17e-09 ***
## edad -0.3242 0.1187 -2.732 0.011 *
## sexohombre 2.6465 1.8776 1.410 0.170
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.713 on 27 degrees of freedom
## Multiple R-squared: 0.2604, Adjusted R-squared: 0.2056
## F-statistic: 4.752 on 2 and 27 DF, p-value: 0.01705Estos resultados indican que el género tiene un efecto protector sobre el deterioro de la memoria semántica en las personas mayores. Comparando hombres y mujeres de la misma edad, las mujeres obtendrán una menor puntuación que los hombres en el test de denominación de Boston.
6.3.1 Selección de modelos
Cuando se construye un modelo es deseable encontrar el mejor subconjunto de predictores que expliquen los datos de manera aceptable. Existen dos estrategias para la selección de variables (Ugarte et al., 2008): 1) mediante la estimación de todos los modelos, y 2) mediante un procedimiento de pasos sucesivos.
6.3.1.1 Estimación de todos los modelos
Es un método que requiere el uso intensivo del ordenador, ya que cuando el número de variables es relativamente grande resulta difícil poder llevarlo a cabo de manera manual. Se elige el modelo que presenta el mejor criterio de ajuste. Ugarte et al. (2008) consideran como criterios válidos el estadístico \(R^{2}\) ajustado o el índice \(C_{p}\). El programa R (R Core Team, 2016) permite calcular todos los modelos posibles.
Para ver este procedimiento seguiremos con el mismo ejemplo y calcularemos todos los modelos de regresión posibles para estudiar el efecto de la edad, la educación y las AEC sobre la puntuación en la primera medida del test de Boston. Los resultados obtenidos son los siguientes:
## Subset selection object
## Call: regsubsets.formula(BOSTON1 ~ edad + edu + AEC, data = dat)
## 3 Variables (and intercept)
## Forced in Forced out
## edad FALSE FALSE
## edu FALSE FALSE
## AEC FALSE FALSE
## 1 subsets of each size up to 3
## Selection Algorithm: exhaustive
## edad edu AEC
## 1 ( 1 ) "*" " " " "
## 2 ( 1 ) "*" "*" " "
## 3 ( 1 ) "*" "*" "*"## [1] 0.1775712 0.2545712 0.2489539Se aprecia en la tabla que el modelo con mejor ajuste (\(R^{2}\)) es el que incluye sólo las variables edad y educación (\(R^{2}\) ajustado = 0.255). El modelo que incluyó sólo la edad presenta un \(R^{2}\) ajustado de 0.178. Es decir, la variable edad explica aproximadamente un 17,8% de la varianza de la variable puntuación en el test de Boston en la primera medición. Estos resultados contrastan con los obtenidos con el modelo que incluyó dos variables (edad y educación) cuyo valor de \(R^{2}\) ajustado fue mayor (0.255). Una forma de valorar esta contribución consiste en cuantificar el grado de cambio al incorporar (eliminar) una variable a la ecuación:
\[ R_{cambio|X_{j}}^{2} = R_{12 \ldots p}^{2}-R_{12 \ldots p-1}^{2} = 0.255-0.178= 0.077 \]
La significación estadística del cambio en \(R^{2}\) viene dada por la siguiente expresión:
\[ F_{cambio|X_{j}}= \frac{R_{cambio|X_{j}}^{2}(n-p-1)}{1 - R_{12 \ldots p}^{2}} = \frac{0.077*(30-2-1)}{1-0.255}=2.79 \]
Comparando este resultado con el de las tablas para una F con 1 y grados de libertad y un nivel de significación del 0.05 obtenemos un valor de F(1,27) = 4.21. Por tanto, a pesar de aumentar el índice de ajuste, éste incremento no resulta ser significativo por lo que el modelo óptimo no cambia. Introducir la variable educación en el modelo no mejora significativamente el ajuste. Si calculamos la raiz cuadrada de 2.79 obtenemos el valor del estadístico t correspondiente al parámetro beta de la variable educación tal y como puede observarse en la siguiente tabla:
##
## Call:
## lm(formula = BOSTON1 ~ edad + edu, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.4374 -2.7496 -0.2429 2.8433 8.2001
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 66.2679 8.3251 7.960 1.48e-08 ***
## edad -0.2921 0.1162 -2.514 0.0182 *
## edu 0.3424 0.1736 1.973 0.0588 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.565 on 27 degrees of freedom
## Multiple R-squared: 0.306, Adjusted R-squared: 0.2546
## F-statistic: 5.952 on 2 and 27 DF, p-value: 0.00722Mediante este procedimiento sólo se incluye la variable edad, ya que es la única que cumple el criterio de significación (\(p(F) \leq.05)\). El resto de variables son excluidas por no cumplir dicho criterio.
El método de selección hacia atrás comienza con el modelo máximo. En cada paso, se elimina aquel predictor que cumple el criterio de eliminación (p(F)>.05) y con mayor nivel de significación. Este procedimiento continua hasta que todos los predictores presentes en el modelo son significativos o no quedan predictores en el modelo. Utilizando el mismo modelo, pero cambiando la opción de Método por tal y como aparece en la siguiente figura nos encontramos que el programa comienza con el modelo máximo (las tres variables incluidas) y elimina aquellas variables que no cumplen el criterio (p(F)< .1). el resultado final es el mismo que en el caso anterior:
## [1] "edad" "BOSTON1" "BOSTON2" "AEC" "edu"n.model<- lm(BOSTON1~1,data=dat1)
all<- lm(BOSTON1~.,data=dat1)
models<-step(all, scope =formula(all),direction ="backward")## Start: AIC=73.31
## BOSTON1 ~ edad + BOSTON2 + AEC + edu
##
## Df Sum of Sq RSS AIC
## - AEC 1 1.772 249.32 71.526
## - edad 1 2.859 250.40 71.656
## - edu 1 3.714 251.26 71.759
## <none> 247.55 73.312
## - BOSTON2 1 298.341 545.89 95.036
##
## Step: AIC=71.53
## BOSTON1 ~ edad + BOSTON2 + edu
##
## Df Sum of Sq RSS AIC
## - edad 1 1.938 251.26 69.758
## - edu 1 5.109 254.43 70.134
## <none> 249.32 71.526
## - BOSTON2 1 313.325 562.64 93.943
##
## Step: AIC=69.76
## BOSTON1 ~ BOSTON2 + edu
##
## Df Sum of Sq RSS AIC
## - edu 1 5.82 257.07 68.445
## <none> 251.26 69.758
## - BOSTON2 1 443.13 694.39 98.255
##
## Step: AIC=68.44
## BOSTON1 ~ BOSTON2
##
## Df Sum of Sq RSS AIC
## <none> 257.07 68.445
## - BOSTON2 1 553.63 810.70 100.901##
## Call:
## lm(formula = BOSTON1 ~ BOSTON2, data = dat1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -6.4306 -1.8228 0.3171 1.6256 7.0326
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 17.97668 4.14804 4.334 0.000171 ***
## BOSTON2 0.65596 0.08447 7.765 1.85e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.03 on 28 degrees of freedom
## Multiple R-squared: 0.6829, Adjusted R-squared: 0.6716
## F-statistic: 60.3 on 1 and 28 DF, p-value: 1.851e-08El método de selección por pasos sucesivos es una combinación de ambos y que presenta la diferencia de que en este procedimiento una variable que ha salido en una etapa puede volver a entrar en otra. Lo mismo puede decirse para aquellas variables que han entrado en un momento determinado y que pueden salir en una fase posterior (Ato & Vallejo, 2007). Los resultados aplicados al modelo anterior son idénticos.
library(stats)
dat1<- dat[,c(1,5,7,8)]
n.model<- lm(BOSTON1~1,data=dat1)
all<- lm(BOSTON1~.,data=dat1)
models<-step(n.model, scope =formula(all),direction ="both")## Start: AIC=100.9
## BOSTON1 ~ 1
##
## Df Sum of Sq RSS AIC
## + edad 1 166.95 643.75 95.983
## + AEC 1 128.99 681.71 97.702
## + edu 1 116.31 694.39 98.255
## <none> 810.70 100.901
##
## Step: AIC=95.98
## BOSTON1 ~ edad
##
## Df Sum of Sq RSS AIC
## + edu 1 81.110 562.64 93.943
## <none> 643.75 95.983
## + AEC 1 41.194 602.56 96.000
## - edad 1 166.948 810.70 100.901
##
## Step: AIC=93.94
## BOSTON1 ~ edad + edu
##
## Df Sum of Sq RSS AIC
## <none> 562.64 93.943
## + AEC 1 16.756 545.89 95.036
## - edu 1 81.110 643.75 95.983
## - edad 1 131.747 694.39 98.255##
## Call:
## lm(formula = BOSTON1 ~ edad + edu, data = dat1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.4374 -2.7496 -0.2429 2.8433 8.2001
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 66.2679 8.3251 7.960 1.48e-08 ***
## edad -0.2921 0.1162 -2.514 0.0182 *
## edu 0.3424 0.1736 1.973 0.0588 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.565 on 27 degrees of freedom
## Multiple R-squared: 0.306, Adjusted R-squared: 0.2546
## F-statistic: 5.952 on 2 and 27 DF, p-value: 0.00722En resumen pues, los tres procedimientos obtienen al final un modelo de regresión en el que la única variable predictora significativa es la edad. Los resultados finales del modelo se incluyen en la siguiente tabla:
6.3.2 Importancia de las variables
No existe un criterio unívoco para determinar la importancia de una variable en el modelo de regresión. En ocasiones, se considera como más importante el que una variable contribuya en mayor medida al cambio esperado en la variable Y. En este caso, la importancia de las variables se puede establecer en base a los coeficientes de regresión tipificados (Pardo & San Martin, 2011). Sin embargo, también puede utilizarse el criterio de aquella variable que más contribuye al ajuste global. Si es el caso, entonces ha de utilizarse el cuadrado del coeficiente de correlación semiparcial para determinar la importancia de cada variable.