6.2 Regresión simple

El modelo de regresión simple es:

\[ Y_{i}= \beta_{0} + \beta_{1}* x_{i} + \epsilon_{i} \]

donde \(Y_{i}\) es el valor de la respuesta del sujeto , \(\beta_{0}\) y \(\beta_{1}\) son los parámetros de la recta de regresión, \(x_{i}\) es el valor del sujeto en la variable predictora. Por último, \(\epsilon_{i}\) es el término de error correspondiente al sujeto .

Este modelo de regresión pretende relacionar dos variables de manera lineal. De hecho, la ecuación de la recta de regresión no es otra cosa que la ecuación de una recta que presenta la propiedad de ser la que menor error produce a la hora de representar las puntuaciones de los sujetos. A la variable X se le denomina variable o variable y a la variable Y se le denomina variable o .

El valor del parámetro \(\beta_{0}\) nos indica el punto de corte de la recta de regresión sobre el eje de ordenadas. En cambio, el valor del parametro \(\beta_{1}\) nos indica la pendiente de la recta. Si este parámetro vale cero nos encontramos con la ausencia de relación entre las dos variables. Asimismo, si este parámetro es de signo negativo tenemos una relación de tipo . Por el contrario, si el parámetro es positivo tendremos una relación entre las dos variables.

Utilizando la base de datos anterior vamos a estudiar las relaciones entre la edad y la puntuación en el test de Boston en la primera medición. Asimismo, queremos estudiar si están relacionadas las dos medidas del Boston.

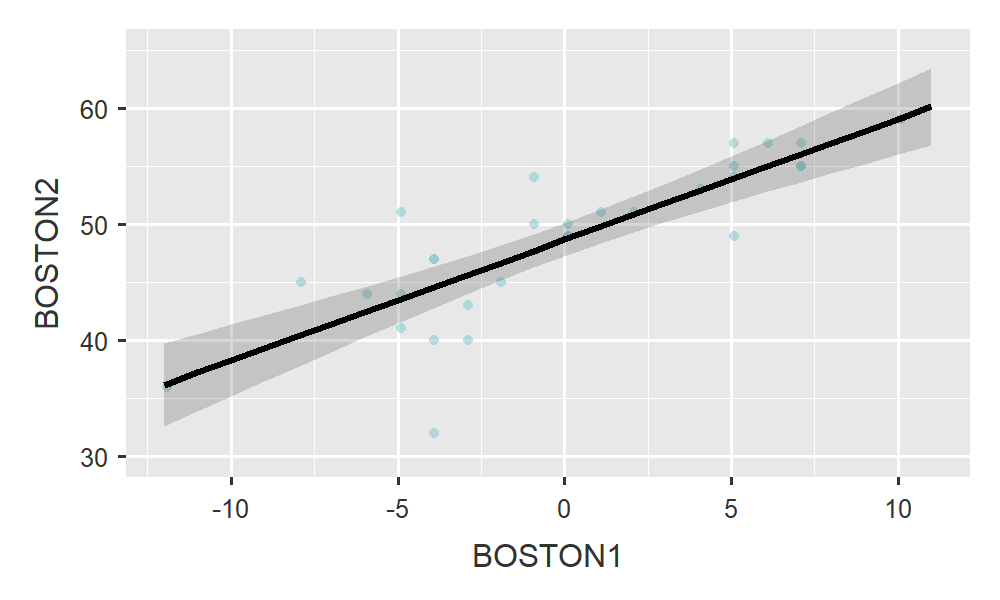
Figura 6.2: Relación entre las medidas de BOSTON2 y BOSTON1

Podemos observar que entre las dos variables de la figura 1 existe una relación lineal de tipo . Es decir, a medida que aumenta la edad, los sujetos tienden a obtener una menor puntuación en el test de Boston.

La recta de regresión obtenida para la figura 1 es:

## 
## Call:
## lm(formula = BOSTON1 ~ edad, data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -7.3598 -3.5486  0.0686  3.1163  9.2432 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  71.9060     8.2132   8.755 1.66e-09 ***
## edad         -0.3254     0.1207  -2.695   0.0118 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.795 on 28 degrees of freedom
## Multiple R-squared:  0.2059, Adjusted R-squared:  0.1776 
## F-statistic: 7.261 on 1 and 28 DF,  p-value: 0.01178

En otras ocasiones nos encontraremos con relaciones directas como en el caso de la figura 2. Se obtiene que a medida que aumenta la puntuación en el primer momento del Boston también aumenta la puntuación obtenida en el Boston en el momento 2. La recta de regresión obtenida para la figura 2 es:

## 
## Call:
## lm(formula = BOSTON2 ~ BOSTON1, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -12.6065  -1.0583   0.2292   1.8560   7.4346 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -3.2830     6.7261  -0.488    0.629    
## BOSTON1       1.0411     0.1341   7.765 1.85e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.817 on 28 degrees of freedom
## Multiple R-squared:  0.6829, Adjusted R-squared:  0.6716 
## F-statistic:  60.3 on 1 and 28 DF,  p-value: 1.851e-08

En ambos casos el parámetro \(\beta_{1}\) es significativo. La única diferencia es que en la relación de la figura 2 el valor es negativo (- 0.325) y en el de la figura 2 positivo (1.041). En el caso de la figura 2, la recta de regresión obtenida es:

\[ \hat{Y}_{i} = 71.90 - 0.325 *x_{i} \]

Según estos resultados, el punto de corte de la recta con el eje de ordenadas está en 71.9 y a medida que las personas aumentan un año de edad su puntuación en el test de Boston disminuye 0.325 unidades.

6.2.1 Predictores categóricos

En el modelo de regresión las variables predictoras pueden ser cuantitativas o cualitativas. Un ejemplo de variable cualitativa puede ser el género. Los resultados del modelo de regresión que relaciona el género con la puntuación en el test de Boston aparece en la siguiente tabla:

## 
## Call:
## lm(formula = BOSTON1 ~ sexo, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -13.7778  -3.0952  -0.4365   5.1429   8.2222 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   49.095      1.141  43.032   <2e-16 ***
## sexohombre     2.683      2.083   1.288    0.208    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5.228 on 28 degrees of freedom
## Multiple R-squared:  0.05592,    Adjusted R-squared:  0.0222 
## F-statistic: 1.659 on 1 and 28 DF,  p-value: 0.2083

Observamos que la recta de regresión obtenida es:

\[ Y_{j} = 49,10 + 2,68* sexo \hspace{15mm} para\; hombres \;y \] \[ Y_{j} = 49,10 \hspace{35mm} para\; mujeres \] Como la variable sexo se ha categorizado como 0 si la persona es mujer y 1 si es hombre el valor esperado en la prueba de Boston será mayor para los hombres que para las mujeres. O lo que es lo mismo, la “intercept” de la ecuación de regresión se corresponde con el valor medio de las mujeres en el test de Boston. Esta es la codificación recomendable para facilitar la interpretación del modelo. Sin embargo, cualquier otra codificación es posible. No obstante, Hayes (2013) recomienda usar valores cuya diferencia entre los valores sea igual a 1. De este modo, el coeficiente \(\beta_{1}\) se podrá interpretar como la diferencia existente entre las medias de los dos grupos.

6.2.2 Realización de pronósticos

Una de las utilidades del modelo de regresión es la de permitir realizar predicciones. Continuando con el ejemplo 1, puede interesarnos conocer la puntuación que obtendría en el test de Boston una persona con 70 años. Utilizando la recta de regresión obtendríamos:

\[ 49.15 = 71.90 - 0.325*70 \]

Esta estimación representa el valor más probable, pero puede interesarnos realizar una estimación mediante intervalos de confianza. Pueden construirse dos tipos de intervalos dependiendo de que queramos realizar estimaciones con respecto a la media o con respecto al individuo. En el primer caso, la estimación se hace para todos los sujetos que tienen una misma puntuación. En cambio, cuando nos interesa realizar un pronóstico individual el pronóstico se interpreta como la estimación asignada a un sujeto concreto con un valor concreto en la variable predictora (Pardo & San Martin, 2011). Estas estimaciones son más amplias que las de la media. La siguiente expresión nos permiten calcular el intervalo de confianza (IC) para los pronósticos individuales:

\[ S_{\hat{Y_{i}}|X_{i}}^{2} = MCE[1+\frac{1}{n}+(X_{i}-\bar{X})^2/\sum (X_{i}-\bar{X})^2] \]

Para el pronóstico con respecto a la media será la siguiente expresión:

\[ S_{\hat{\mu_{i}}|X_{i}}^{2} = MCE[\frac{1}{n}+(X_{i}-\bar{X})^2/\sum (X_{i}-\bar{X})^2] \]

Aplicados a los datos de nuestro ejemplo obtenemos (47,24;51,02) para el IC de la media y (39,13;59,13) para el pronóstico individual. Queda manifiesto que los pronósticos individuales son menos exactos que los referidos a la media.