2.8 Prueba de Kuskal-Wallis (KW)
Esta prueba no necesita que se cumplan los supuestos de normalidad y homogeneidad propias del ANOVA. Además, puede utilizarse cuando los datos son de tipo ordinal. Este método pretende contrastar la hipótesis de que J muestras aleatorias independientes proceden de la misma población (o de distintas poblaciones). Para ello, se asignan rangos desde 1 hasta N al conjunto de las \(Y_{ij}\) observaciones del diseño como si fuera un única muestra (si hay empates se aplica el promedio de los rangos implicados). Al final se obtiene un rango \(R_{ij}\) para cada una de las observaciones.
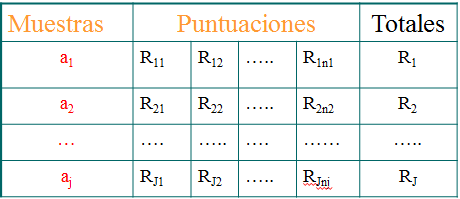
Figura 2.4: Esquema del diseño para la prueba de Kruskall-Wallis
El estadístico H de Kruskal-Wallis viene definido de la siguiente forma:
\[ H = \frac{12}{N(N+1)}\sum_{j=1}^{J}\frac{R_j}{n_j} - 3(N - 1) \]
Bajo la hipótesis nula de que las J poblaciones tienen la misma forma, el estadístico H se distribuye según un modelo de probabilidad ji-cuadrado con J - 1 grados de libertad. El rechazo de esta hipótesis supone que los J promedios comparados no son iguales.
Ejemplo 2.2:
Supongamos que estamos interesados en el estudio de los 3 métodos de enseñanza para mejorar el rendimiento de los escolares. Los resultados fueron los siguientes:
| A | B | C | |
|---|---|---|---|
| s1 | 26 | 22 | 7 |
| s2 | 35 | 5 | 7 |
| s3 | 17 | 22 | 18 |
| s4 | 23 | 21 | 6 |
| s5 | 24 | 20 | 12 |
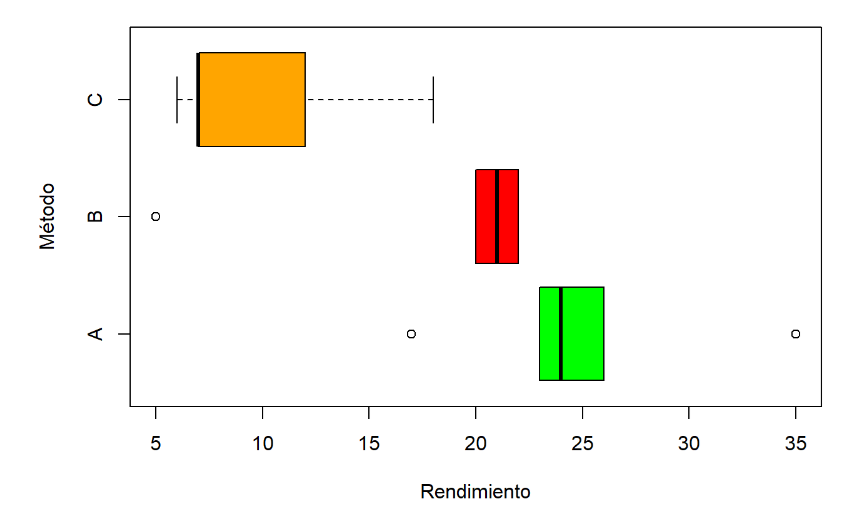
Figura 2.5: Boxplot del ejemplo 2.2
Observamos que los grupos son bastante asimétricos. En particular, se tiene que el grupo B muestra una distribución muy alejada de la normalidad. Esto puede comprobarse mediante el estadístico de Shapiro-Wilk:
Media del grupo A:
##
## Shapiro-Wilk normality test
##
## data: aciertos2[1:5]
## W = 0.94691, p-value = 0.7151Media del grupo B:
##
## Shapiro-Wilk normality test
##
## data: aciertos2[6:10]
## W = 0.64863, p-value = 0.002565Media del grupo C:
##
## Shapiro-Wilk normality test
##
## data: aciertos2[11:15]
## W = 0.82664, p-value = 0.1313En este caso es adecuado aplicar el estadístico de Kruskal- Wallis.
Kruskal-Wallis rank sum testdata: aciertos2 by grupo Kruskal-Wallis chi-squared = 7.6473, df = 2, p-value = 0.02185
| A | B | C | |
|---|---|---|---|
| s1 | 14 | 10.5 | 3.5 |
| s2 | 15 | 1.0 | 3.5 |
| s3 | 6 | 10.5 | 7.0 |
| s4 | 12 | 9.0 | 2.0 |
| s5 | 13 | 8.0 | 5.0 |
En la tabla 2.5 aparece el rango para cada una de las puntuaciones. Calculando las medias de los rangos de cada uno de los grupos observamos que las menores puntuaciones están en el grupo C seguido del grupo B:
Media del grupo A:
## [1] 12Media del grupo B:
## [1] 7.8Media del grupo C:
## [1] 4.2Al igual que en el caso del ANOVA, para conocer cuáles son las diferencias significativas entre los grupos será necesario realizar una prueba post-hoc.
2.8.1 Comparaciones a posteriori
Cuando no se cumplen los supuestos de aplicación del ANOVA las comparaciones a posteriori se pueden realizar mediante la técnica U de Mann-Whitney (MW)4. Esta prueba sirve, al igual que la prueba T de Student para comparar dos muestras independientes. Resulta útil cuando no se cumple la hipótesis de normalidad o los datos son ordinales.
Sean dos muestras aleatorias de tamaño \(n_1\) y \(n_2\). Sea \(R_{i}\) el rango asignado a cada una de las puntuaciones cuando se toman todas en conjunto como si fuera una única muestra. A continuación, se calculan los siguientes estadísticos \(S_1\) y \(S_2\) que corresponden a la suma de los rangos de las observaciones del grupo 1 y grupo 2 respectivamente:
\[ S_1 = \sum_{i=1}^{n_1}R_{i1} \qquad y \qquad S_2 = \sum_{i=1}^{n_2}R_{i2} \] Se verifica que la suma de los N rangos vale (Pardo & San Martin, 2010):
\[ S_1 + S_2 = \frac{N(N+1)}{2} \]
Si se asume que las dos muestras proceden de la misma población cabe esperar que \(S_1\) y \(S_2\) sean iguales o parecidos y que solo muestren pequeñas variaciones debidas al azar. Por tanto, el estadístico U sería cualquiera de los dos sumandos. Por ejemplo, U = \(S_1\).
Una vez definido el estadístico, el paso siguiente es determinar su distribución de probabilidad. Esta distribución no es muy complicada en el caso de que tengamos pocos valores y podremos calcular el valor de probabilidad exacto. Cuando el número de valores es relativamente grande será necesario realizar la siguiente aproximación:
\[ Z = \frac{U - \mu_U}{\sigma_U} \qquad donde \qquad \mu_U = \frac{n_1(N+1)}{2} \qquad y \qquad \sigma_U = \sqrt{n_1n_2(N+1)/12} \] Ejemplo
En el ejemplo 2.2 que se estudió cuando se introdujo la técnicas KW encontramos que había diferencias significativas por lo que será necesario determinar las diferencias entre los distintos métodos de enseñanza. Necesitamos determinar que métodos son los que muestran diferencias significativas:
Prueba de U de Mann-whitney para métodos A y B:
##
## Wilcoxon rank sum test with continuity correction
##
## data: b[1:5] and b[6:10]
## W = 21, p-value = 0.09369
## alternative hypothesis: true location shift is not equal to 0Tamaño del efecto para métodos A y B:
##
## Cliff's Delta
##
## delta estimate: 0.68 (large)
## 95 percent confidence interval:
## lower upper
## -0.2847567 0.9604032Prueba de U de Mann-whitney para métodos A y C:
##
## Wilcoxon rank sum test with continuity correction
##
## data: b[1:5] and b[11:15]
## W = 24, p-value = 0.02118
## alternative hypothesis: true location shift is not equal to 0Tamaño del efecto para métodos A y C:
##
## Cliff's Delta
##
## delta estimate: 0.92 (large)
## 95 percent confidence interval:
## lower upper
## 0.5171092 0.9891504Prueba de U de Mann-whitney para métodos B y C:
##
## Wilcoxon rank sum test with continuity correction
##
## data: b[6:10] and b[11:15]
## W = 20, p-value = 0.1412
## alternative hypothesis: true location shift is not equal to 0Tamaño del efecto para métodos B y C:
##
## Cliff's Delta
##
## delta estimate: 0.6 (large)
## 95 percent confidence interval:
## lower upper
## -0.4370519 0.9522030Si consideramos un criterio de significación \(\alpha\) = 0,05 tenemos que corregir el azar debido a que hemos realizado más de un test. Aplicando el criterio de Bonferroni (\(\alpha_C\) = 0,05/3 = 0.0167) concluimos que no hay ninguna diferencia significativa. La misma conclusión obtendríamos si aplicáramos la corrección de Sidak (\(\alpha_C\) = 0,017).
El problema de utilizar la prueba de U de Mann-Whitney para realizar las comparaciones a posteriori es que no se mantienen los rangos del conjunto de observaciones, produciéndose un reajuste de los rangos en cada una de las comparaciones dos a dos. Existen varias alternativas a este procedimiento como la prueba de Dunn, la de Conover, el test de Nemenyi o la prueba de Dwass-Steel-Critchlow-Fligner (DSCF). En el programa de JAMOVI las comparaciones a posteriori se realizan mediante la prueba de DSCF. Se considera que un contraste es significativo si satisface:
\[ W_j = -\frac{n_i(ni+n_j+1)}{2}/\frac{n_in_j}{24}\times \Lambda > q_{\alpha,k}, \quad \text{para} \quad 1\leq i\leq j\leq k \]
donde:
\[ \Lambda = n_i+n_j -1-\frac{\sum_{b=1}^{g_{ij}}{(t_{b}-1)tb(t_{b}+1)}}{(n_i +n_j)(n_i+n_j -1)} \]
\(q_{\alpha,k}\) es una cuantila de la distribución normal de los rangos para k grupos, \(n_i\) es el número de sujetos del i-ésimo grupo, \(n_j\) es el número de sujetos del j-ésimo grupo, \(t_b\) es el número de ocurrencias en el rango b y \(W_{ij}\) es la suma de los rangos para el i-ésimo grupo donde los rangos se han comparado con el grupo j. Los resultados de aplicar esta prueba aparecen a continuación. Encontramos que sólo aparecen diferencias entre los grupos A y C.
## A B
## B 0.176 -
## C 0.042 0.256JAMOVI utiliza la prueba de Dwass-Steel-Critchlow-Fligner↩︎