4.2 Interacción entre factores
Conceptualmente podemos considerar que la interacción entre factores hace referencia a que el efecto de una VI sobre la VD depende del valor que está presente de la otra VI. Ahora bien, desde un punto de vista más formal el efecto interactivo se define de la siguiente forma:
\[ \alpha\beta_{jk}= \mu_{jk} - (\mu_{++} + \alpha_{j} + \beta_k) \]
Existe interacción cuando \(\alpha\beta_{jk} \neq\) 0 para algún jk. Pardo & San Martin (2010) consideran que esta expresión puede interpretarse de dos formas:
Como desviación que experimentan las medias de las casillas con respecto a los efectos principales de los factores:
- No interacción: \(\mu_{jk} = \mu_{j+} \mu_{+k} - \mu_{++}\) (para todo j y k)
- Interacción: \(\mu_{jk} \neq \mu_{j+} \mu_{+k} - \mu_{++}\) (para todo j y k)
Como diferencias entre las medias de las casillas y las medias marginales:
- No interacción: \(\mu_{jk} - \mu_{j'k} = \mu_{j+} - \mu_{j'+}\) (para todo j, j’ ó k)
- Interacción: \(\mu_{jk} - \mu_{j'k} \neq \mu_{j+} - \mu_{j'+}\) (para todo j, j’ ó k)
Estas dos conceptualizaciones del efecto interactivo al final se traducen en el concepto anteriormente mencionado de la existencia de interacción siempre y cuando las diferencias de un factor (p. ejemplo, el factor A), son distintas dependiendo del valor que está presente del otro factor B. En la siguiente figura se presentan dos situaciones donde en la primera de ellas no existe interacción entre las variables y en la otra si.

Figura 4.2: Medias de dos diseños factoriales con y sin interacción
Gráficamente es muy fácil apreciar la existencia (o no) de interacción: cuando las líneas son paralelas no existe interacción. Por el contrario, si las líneas se cruzan o no son paralelas hablamos de interacción. En la figura 3 izquierda se observa con claridad que cualquier valor del factor B cambia en 2 unidades siempre, dependiendo de que esté presente el valor de \(a_1\) o \(a_2\). En cambio, en la figura de la derecha los cambios no son uniformes. Son mucho más elevados cuando el valor de B es \(b_2\) que cuando el valor de B es \(b_1\) ó \(b_3\). Es más, se observa que el cambio significativo en el factor A es sólo cuando está presente \(b_2\). Cuando están presentes los otros valores de B los cambios son muy parecidos.
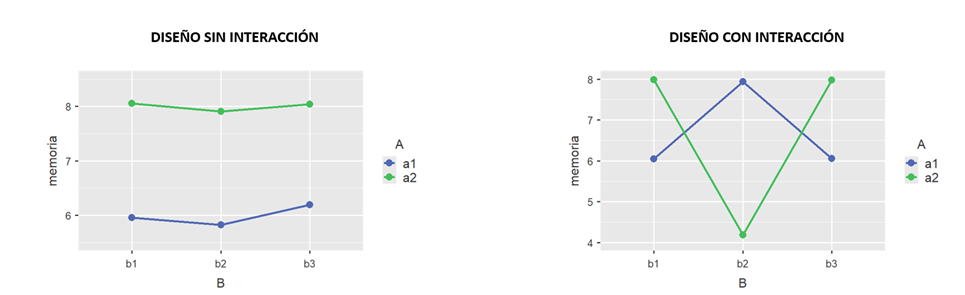
Figura 4.3: Representación gráfica de dos diseños factoriales sin y con interacción
4.2.1 Ejemplo 4.1 de diseño factorial
Supongamos que estamos interesados en estudiar si el efecto de la dieta (\(a_1\) = Dieta A, \(a_2\) = Dieta B) sobre la actividad motora depende de las horas de sueño \(b_1\) = 2 horas, \(b_2\) = 4 horas y \(b_3\) = 6 horas). Los resultados de los sujetos aparecen a continuación:
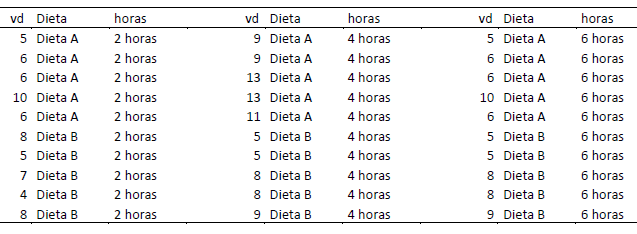
Figura 4.4: Datos del ejemplo 4.1
Analizando estos datos nos encontramos que existe un efecto interactivo entre la variable tipo de dieta y horas de sueño (ver tabla 4.1). Asimismo, podemos comprobar mediante el estadístico de Levene que se cumple el supuesto de homogeneidad (ver tabla 4.2).
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| horas | 2 | 37.27 | 18.63 | 5.11 | 0.01 |
| Dieta | 1 | 12.03 | 12.03 | 3.30 | 0.08 |
| horas:Dieta | 2 | 28.47 | 14.23 | 3.90 | 0.03 |
| Residuals | 24 | 87.60 | 3.65 | NA | NA |
| Df | F value | Pr(>F) | |
|---|---|---|---|
| group | 5 | 0.14 | 0.98 |
| 24 | NA | NA |
En la siguiente figura observamos que el efecto de la dieta sobre la actividad motora es prácticamente inexistente cuando los animales durmieron 2 o 6 horas. Sin embargo, se produce una gran diferencia en la actividad motora con la dieta A cuando los animales durmieron 4 horas (condición \(a_1b_2\)).
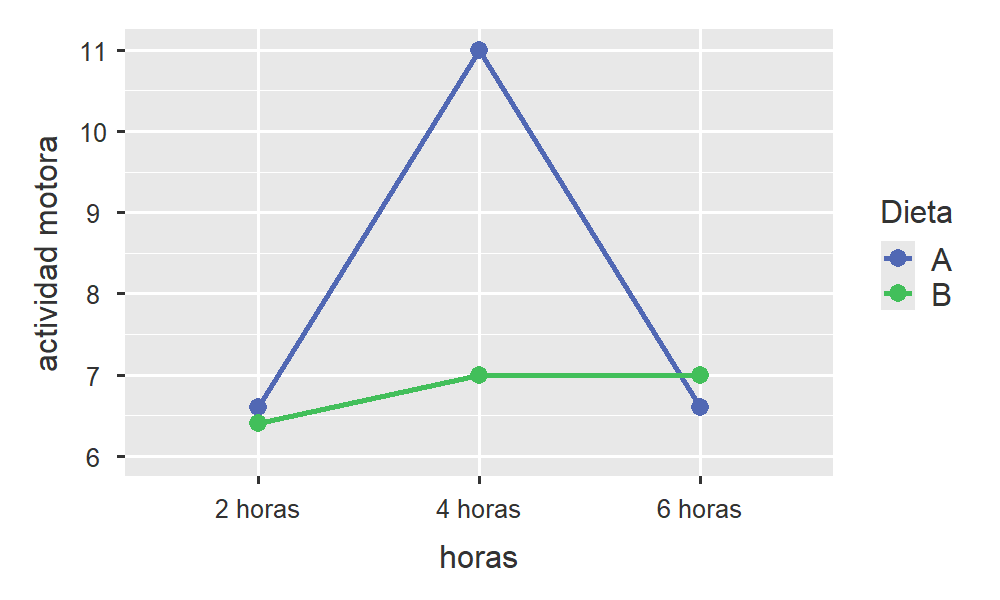
Figura 4.5: Representación gráfica del ejemplo 4.1
4.2.1.1 Cálculo de los efectos simples
Una vez que se constata la existencia de interacción en el diseño, el paso siguiente consiste en interpretar la interacción mediante la comparación de los efectos simples. Un efecto simple calcula la diferencia de dos valores de la VD en presencia de dos valores distintos de la VI, manteniendo constante el valor de una tercera. Consideremos los valores medios de nuestro ejemplo 1:
| \(a_1b_1\) | \(a_2b_1\) | \(a_1b_2\) | \(a_2b_2\) | \(a_1b_3\) | \(a_2b_3\) | |
|---|---|---|---|---|---|---|
| Medias | 6.6 | 11 | 6.6 | 6.4 | 7 | 7 |
Los efectos simples de la variable dieta serían:
- Comparar los valores medios de las dieta A con la dieta B cuando los animales durmieron 2 horas:
\[ Efecto \; simple \; de \; A = \overline{X}_{a_1b_1}- \overline{X}_{a_2b_1} = 6.6 - 6.4 = 0.2 \]
- Comparar los valores medios de las dieta A con la dieta B cuando los animales durmieron 4 horas:
\[ Efecto \; simple \; de \; A = \overline{X}_{a_1b_2} - \overline{X}_{a_2b_2} = 11 - 7 = 4 \]
- Comparar los valores medios de las dieta A con la dieta B cuando los animales durmieron 6 horas:
\[ Efecto \; simple \; de \; A = \overline{X}_{a_1b_3} - \overline{X}_{a_2b_3} = 6.6 - 7 = -0.4 \]
Para determinar el efecto de la interacción necesitamos comparar entre sí todos estos efectos simples. Así, en este diseño tendremos tres comparaciones:
- Comparación del efecto simple de A (dieta) en \(b_1\) (2 horas de sueño) con el efecto simple de A en \(b_2\) (4 horas de sueño):
\[ \phi_1 = \overline{X}_{a_1b_1}- \overline{X}_{a_2b_1} - (\overline{X}_{a_1b_2}- \overline{X}_{a_2b_2}) = 6.6 - 6.4 - 11 + 7 = -3.8 \]
- Comparación del efecto simple de A (dieta) en \(b_1\) (2 horas de sueño) con el efecto simple de A en \(b_3\) (6 horas de sueño):
\[ \phi_2 = \overline{X}_{a_1b_1} - \overline{X}_{a_2b_1} - (\overline{X}_{a_1b_3} - \overline{X}_{a_2b_3}) = 6.6 - 6.4 - 6.6 + 7 = 0.6 \]
- Comparación del efecto simple de A (dieta) en \(b_2\) (4 horas de sueño) con el efecto simple de A en \(b_3\) (6 horas de sueño):
\[ \phi_1 = \overline{X}_{a_1b_1} - \overline{X}_{a_2b_1} - (\overline{X}_{a_1b_2}- \overline{X}_{a_2b_2}) = 11 - 7 - 6.6 + 7 = 4.4 \]
Observamos que las diferencias se establecen cuando se comparan los efectos simples de A con el valor \(b_2\) (4 horas de sueño). En los otros las diferencias son pequeñas. No obstante, debemos considerar si esas diferencias encontradas cuando se comparan dos efectos simples se deben al azar. La comparación de los contraste anteriores y la varianza del error permite obtener un estadístico t que se distribuye como una distribución t teórica con 24 grados de libertad. Una estimación de la varianza del error puede hacerse promediando las varianzas de las condiciones del diseño. En nuestro caso, sería:
| \(s_{a_1b_1}\) | \(s_{a_2b_1}\) | \(s_{a_1b_2}\) | \(s_{a_2b_2}\) | \(s_{a_1b_3}\) | \(s_{a_2b_3}\) | |
|---|---|---|---|---|---|---|
| valor | 1.95 | 1.82 | 2 | 1.87 | 1.95 | 1.87 |
\[ Var_{error} = \frac{1.95+1.82+2+1.87+1.95+1.87}{6} = 1.91 \]
Calculando el estadístico t para cada uno de los contrastes:
- Primer contraste:
\[ t = \frac{\phi_1}{Var_{error}} = \frac{-3.8}{1.91} = 1.99 \]
- Segundo contraste:
\[ t = \frac{\phi_2}{Var_{error}} = \frac{0.6}{1.91} = 0.31 \]
- Tercer contraste:
\[ t = \frac{\phi_3}{Var_{error}} = \frac{4.4}{1.91} = 2.30 \]
El estadístico t para un nivel de confianza del 95% tiene un valor de 1.71 por lo que puede considerarse que el primer (\(\phi_1\)) y el tercer contraste (\(\phi_3\)) resultan significativos (F(2,24) = 3.9, p = .034, \(\eta_p\) = 0.298, indicando un tamaño de efecto grande). Observando en la figura apreciamos que el efecto de la dieta con 4 horas de sueño fue significativamente distinto en comparación con el efecto de la dieta a las 2 horas (t(24) = 1.99, p =.029) y 6 horas de sueño (t(24) = 2.30, p =.015).
4.2.2 Ejemplo 4.2 de diseño factorial
Supongamos que estamos interesados en estudiar si la memoria de trabajo de escolares se veía afectada por las variables edad y cantidad de zonas verdes próximas al centro educativo. Para realizar el análisis de los datos debemos asegurarnos de que se cumplen los supuestos de la prueba (normalidad y homogeneidad de las varianzas). En la siguiente figura se representan los datos por condición del estudio.
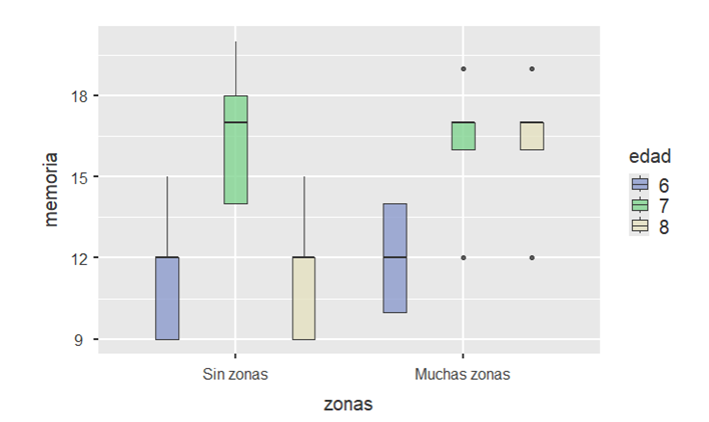
Figura 4.6: Boxplot del ejemplo 4.2
Realizando el análisis de la varianza observamos que la interacción no resulta significativa, siendo la edad el único factor significativo. Por tanto, en este diseño lo único que hay que hacer es determinar si existen diferencias significativas entre las distintas edades. Para ello hay que realizar algún procedimiento post hoc como el de Tukey.
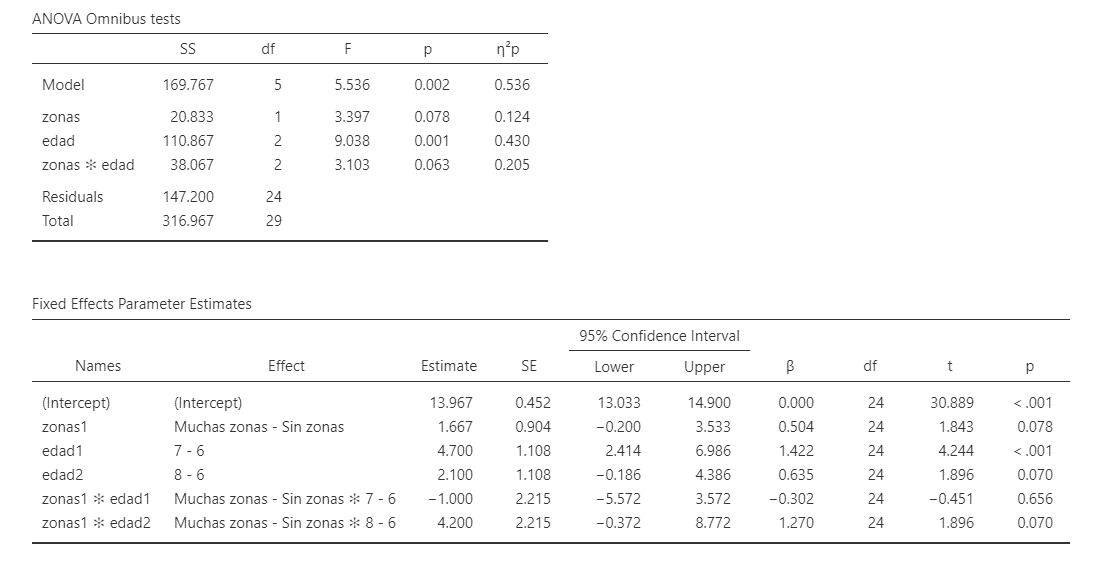
Figura 4.7: Resultados del ejemplo 4.2
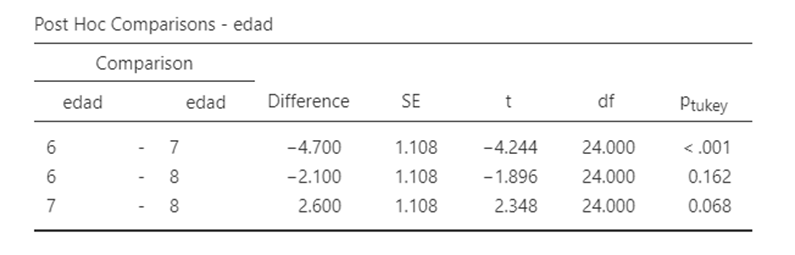
Figura 4.8: Prueba de Tuckey para las comparaciones de edad del ejemplo 4.2
Los resultados indican que sólo hubo un efecto significativo de la edad F(2,24) = 9.04, p = 0.001, \(\eta^2\) parcial = 0.43 indicando un tamaño del efecto grande). Las comparaciones a posteriori de Tukey indicaron que hubo diferencias significativas en la memoria de trabajo a los 6 años (M = 11.40) comparado con los 7 años de edad (M = 16.60, p < .001).