2.9 ANOVA de un factor con JAMOVI

Este programa incluye un módulo específico para las técnicas de ANOVA donde aparecen dos posibilidades para realizar el ANOVA de 1 factor para muestras independientes: 1) Opción one-way ANOVA de un factor y 2) opción ANOVA. Asimismo, incluye en ese módulo la posibilidad de realizar el ANOVA no paramétrico de Kruskal-Wallis.

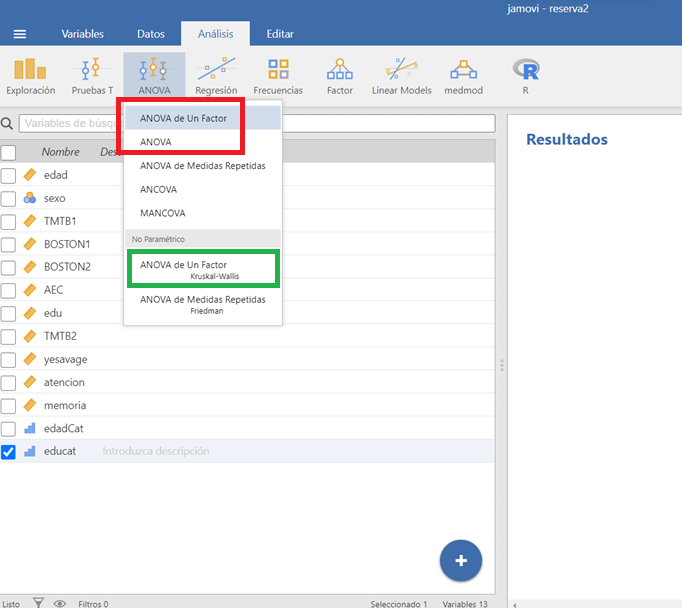
Figura 2.6: Opciones ANOVA en el programa JAMOVI

En la opción “ANOVA de un factor” es posible elegir entre la prueba de Fisher que asume homogeneidad de varianzas y la prueba de Welch que no asume igualdad de las varianzas. En esta opción se pueden introducir más de una VD.

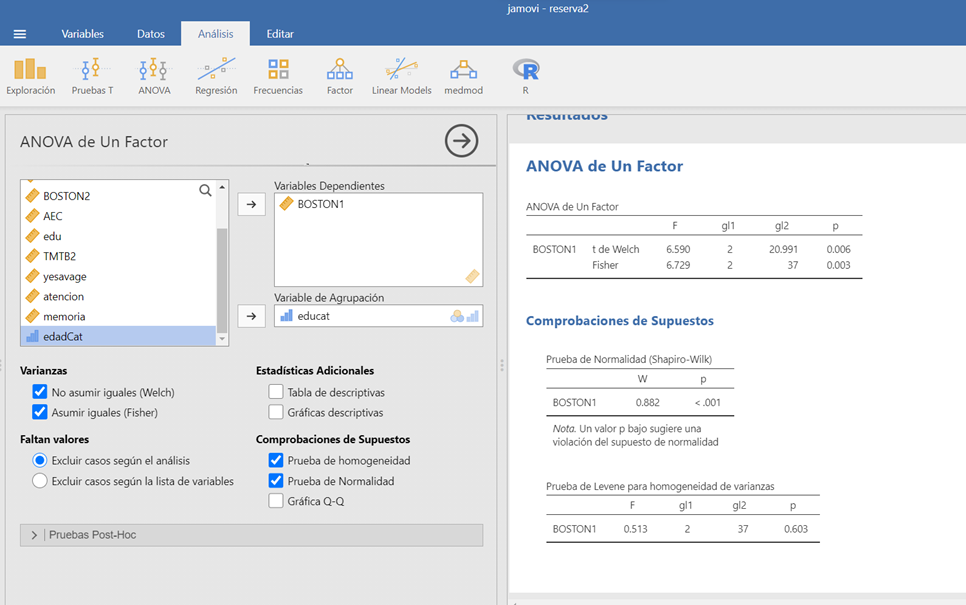
Figura 2.7: Opciones ANOVA en el programa JAMOVI

Asimismo, con esta opción podemos elegir entre distintos métodos de comparación a posteriori tanto para la situación en la que existe homogeneidad de varianzas (Tuckey) como en el caso de que no exista homogeneidad de varianzas (Games-Howell).

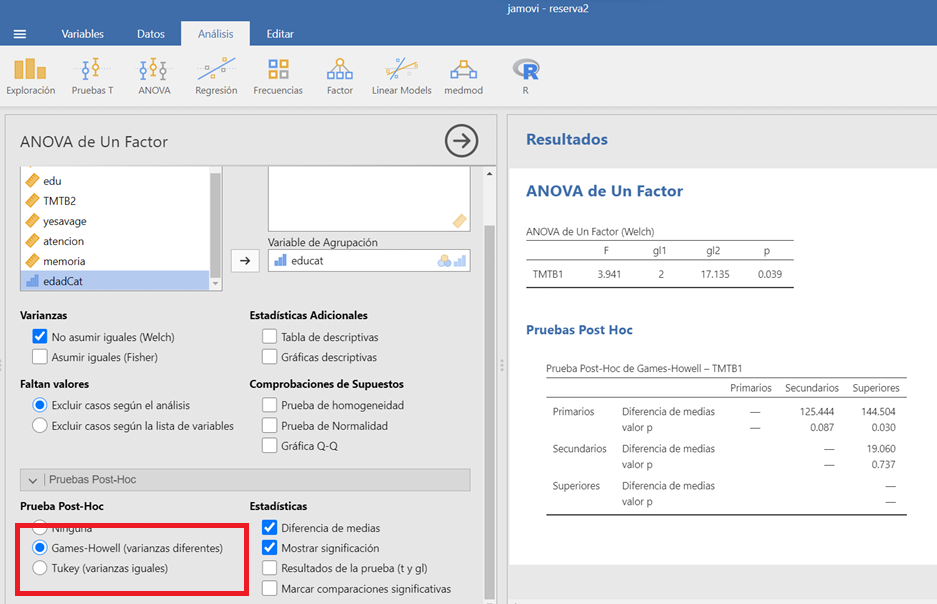
Figura 2.8: Opciones ANOVA en el programa JAMOVI

Si se elige la opción de “ANOVA” sólo estará disponible la posibilidad de comparar grupos con varianzas homogéneas. Sin embargo, esta opción presenta la ventaja de obtener diferentes medidas del tamaño del efecto y pueden incluirse varias VVII para estudiar el efecto de la interacción entre ellas.

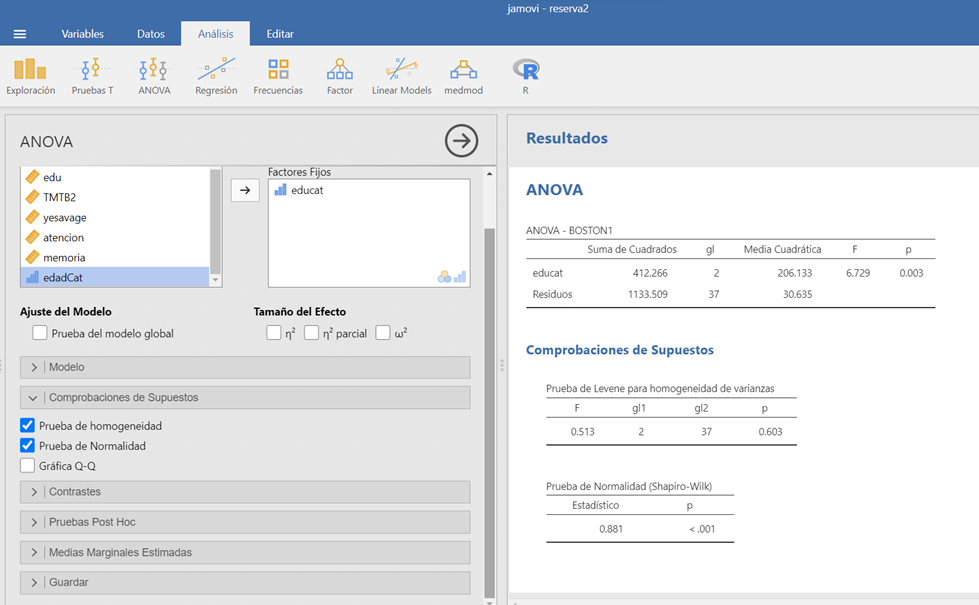
Figura 2.9: Opciones ANOVA en el programa JAMOVI

Si se elige la opción de ANOVA no paramétrico se obtendrá el valor del estadístico K-W así como la medida de tamaño de efecto \(\epsilon^{2}\) y las comparaciones a posteriori de Dwass-Steel-Critchlow-Fligner.

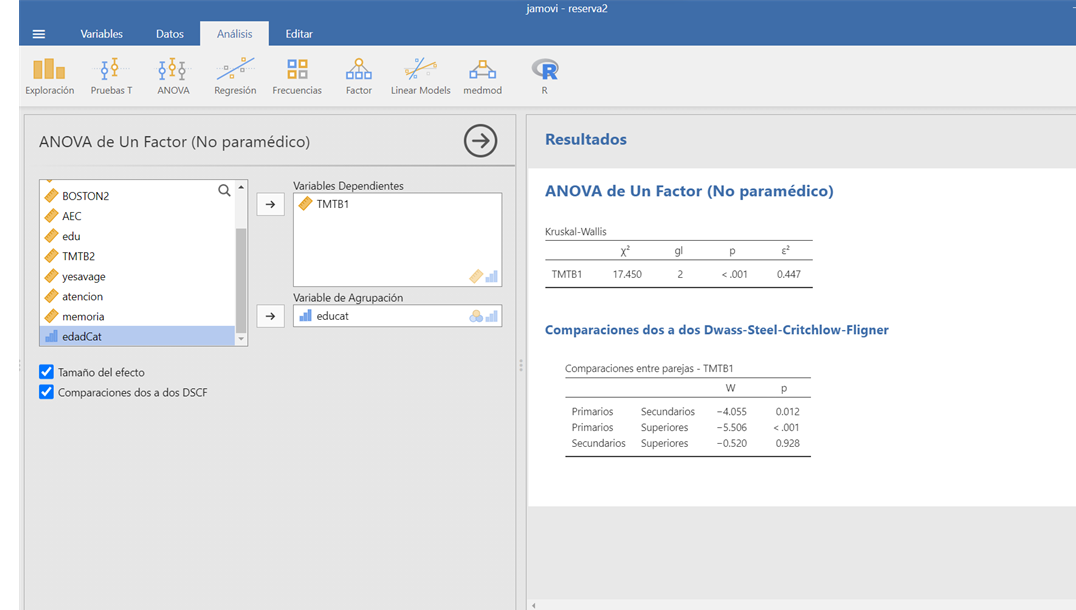
Figura 2.10: Opciones para ANOVA no paramétrico en el programa JAMOVI