5.2 Diseño factorial mixto (A2FMX)
Hay ocasiones en las que interesa al investigador conocer si el efecto de una VI que se ha estudiado mediante medidas repetidas cambia en función de alguna VI de agrupamiento (por ejemplo, diferencias entre hombres y mujeres o diferencias entre grupos de pacientes distintos). A este tipo de diseños se les denomina diseños factoriales mixtos, ya que combinan la estrategia longitudinal con la transversal. El caso más sencillo de estos diseños es el que combina una VI estudiada mediante la estrategia longitudinal y otra VI que se estudia mediante la estrategia transversal.
5.2.1 Ejemplo 2: Diseño factorial mixto
Ilustramos este tipo de diseños con un estudio en el que se realizó un seguimiento de un grupo de pacientes lesionados en distintos momentos del tratamiento. La VI que se estudio de manera longitudinal es el paso del tiempo (inicio, mitad y final); la VI que agrupa a los sujetos es la localización de la lesión (hemisferio izquierdo versus hemisferio derecho). La VD fueron los resultados en una prueba de memoria. En la siguiente tabla se presentan los descriptivos para cada una de las condiciones:
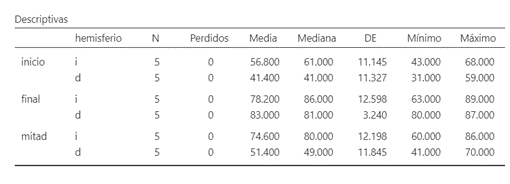
Figura 5.11: Descriptivos del ejemplo 5.2
Una representación gráfica de las medias por condición aparece en la siguiente figura.
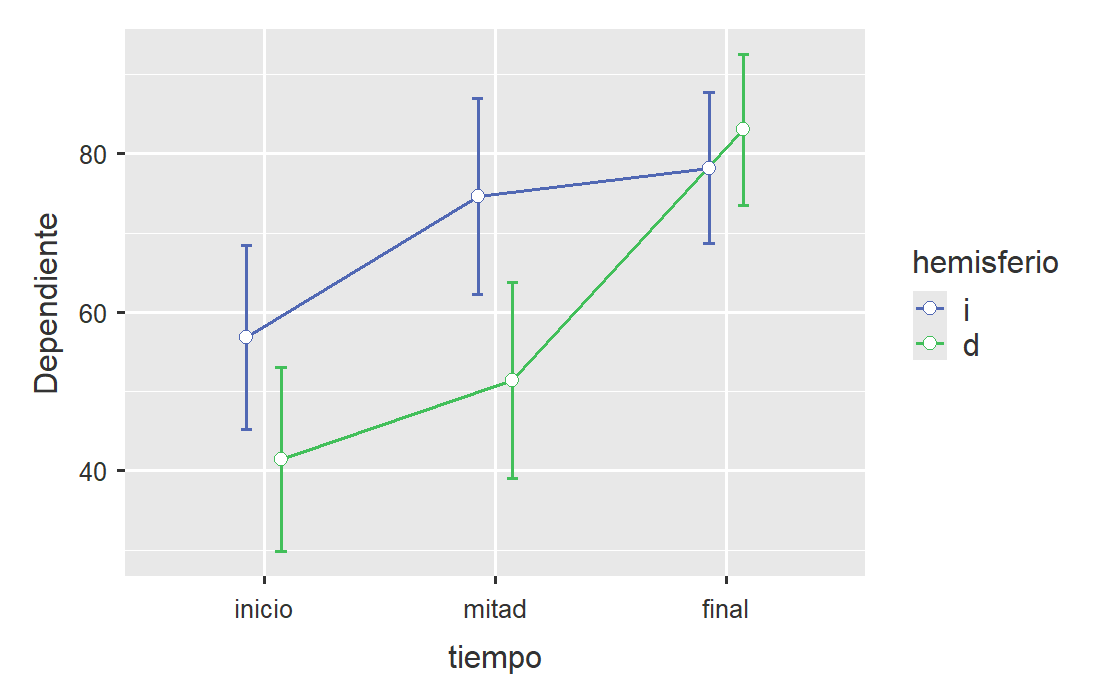
Figura 5.12: Gráfica del ejemplo 5.2
En la figura se aprecia que las diferencias en la prueba entre los dos grupos es pequeña en el momento final. También se aprecia que esas diferencias fueron máximas en la mitad de la intervención.
Los resultados de este ejemplo indican la existencia de una interacción significativa:
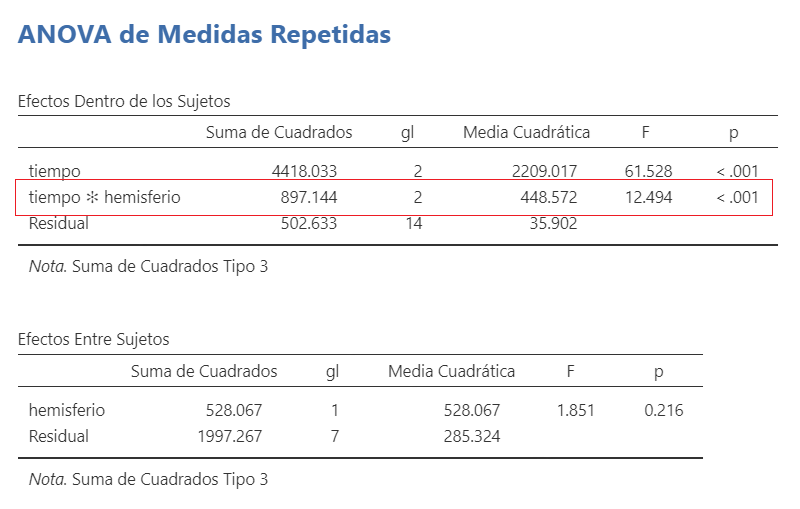
Figura 5.13: Modelo A2FMR en JAMOVI: Resultados del ejemplo 5.2
Para considerar como válidos estos resultados es necesario que se cumplan los supuestos del modelo (normalidad, homogeneidad de varianzas-covarianzas y esfericidad). En relación con el supuesto de esfericidad la prueba de Mauchly confirma su existencia:

Figura 5.14: Modelo A2FMR en JAMOVI: Prueba de esfericidad del ejemplo 5.2
5.2.1.1 Medidas del tamaño del efecto
El estadístico \(\eta^2\) parcial nos permite obtener una estimación del tamaño del efecto aunque ya se ha mencionado que no es un buen estimador siendo preferible utilizar el estadístico \(\omega^2\) o \(\eta_g^{2}\). Para este diseño la fórmula es:
- Para el efecto de A:
\[ \omega_{A}^2 = \frac{gl_A(F_A - 1)}{gl_A(F_A - 1)+ nab} \]
- Para el efecto B:
\[ \omega_{B}^2 = \frac{gl_B(F_B - 1)}{gl_B(F_B - 1)+ nab} \]
- Para el efecto AB:
\[ \omega_{AB}^2 = \frac{gl_{AB}(F_{AB} - 1)}{gl_{AB}(F_{AB} - 1)+ nab} \]
5.2.1.2 Comparaciones múltiples
En el caso de que no resulte signficativo el efecto de la interacción AB y exista algún efecto principal (A y/o B) significativo habrá que continuar realizando las comparaciones a posteriori tal y como se indicó en los temas anteriores. Si el efecto interactivo AB resulta significativo será necesario realizar las comparaciones de los efectos simples. Para ello se calculan las diferencias entre las distintas medidas repetidas. Esas diferencias se comparan entre los distintos grupos tal y como se hizo en el tema 1 para la comparación de muestras independientes. En nuestro caso los resultados aparecen en la siguiente tabla:
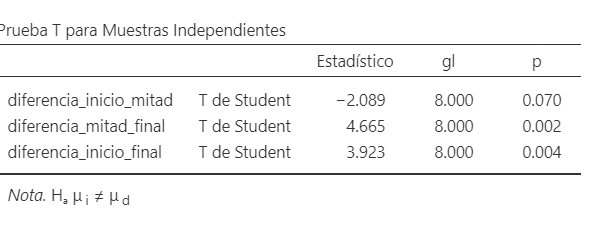
Figura 5.15: Modelo A2FMR en JAMOVI: Comparación de los efectos simples
Encontramos que las comparaciones inicio - final y mitad-menos final fueron significativas. muestran diferencias significativas.
Conclusiones según normas APA: Se encontró la existencia de interacción entre las variables tipo de lesión* y el tiempo (F(2,14) = 12.49, p< .001, \(\eta_p^{2}\) = 0.67, indicando un TE grande). Se encontró que las diferencias en las medidas inicio y final fueron mayores en los pacientes con lesión en el hemisferio derecho (t(8)= 3.92, p = .004). También la diferencia entre la mitad y final del estudio fue mayor en los lesionados en el hemisferio derecho (t(8)= 4.67, p = .002)}.*