5.3 Análisis de los ejemplos con SPSS
5.3.1 Análisis del ejemplo 5.1 con SPSS
Para analizar estos datos mediante el programa SPSS es necesario utilizar la opción Analizar + Modelo lineal general + Medidas repetidas tal y como aparece en la siguiente figura:
Figura 5.16: Selección del modelo A2FMR en SPSS
Al igual que en el tema 3 necesitamos introducir los datos. En este caso debemos indicar que son dos los factores que existen en el diseño uno con dos valores (factor A) y otro con 3 (factor B). Hay que asignar un nombre a cada variable e indicar el número de niveles:
Figura 5.17: Definición de las variables en el modelo A2FMR en SPSS
La prueba de esfericidad nos indica la idoneidad de estos resultados. Podemos observar que los valores de \(\epsilon\) de Geisser-Greenhouse (GG) son más pequeños que los de Huynh-Feldt (HF). Utilizar los valores de GG para realizar los contrastes de hipótesis supone aplicar una estrategia conservadora en el análisis de los datos.

Figura 5.18: Modelo A2FMR: Prueba de esfericidad
En la siguiente figura aparece la tabla ANOVA con los resultados obtenidos en el estudio:
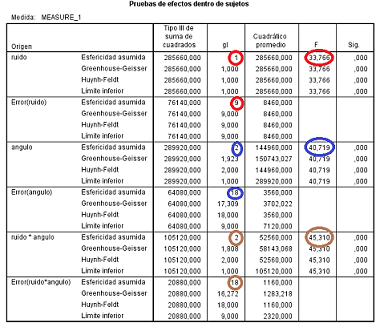
Figura 5.19: Modelo A2FMR en SPSS: Tabla ANOVA
5.3.1.1 Estudio de la interacción
- Creamos las nuevas variables que denominamos “Contraste”. Para el *Contraste1” sería:
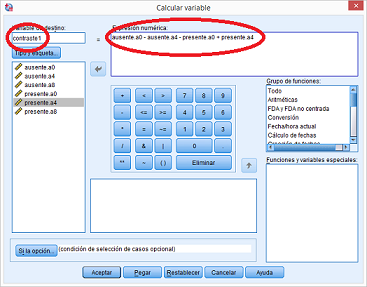
Figura 5.20: Modelo A2FMR en SPSS: Comparación efectos simples
Analizamos esta variable mediante el procedimiento de “Prueba T para una muestra”:
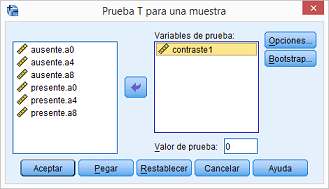
Figura 5.21: Modelo A2FMR en SPSS: Comparación efectos simples: Contraste 1
- Creamos una nueva variable que denominamos Contraste 2 de la siguiente forma:
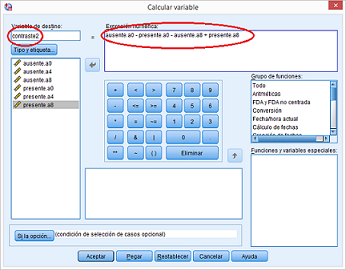
Figura 5.22: Modelo A2FMR en SPSS: Comparación de efectos simples
Los resultados obtenidos con este segundo contraste se muestran en la siguiente figura:

Figura 5.23: Modelo A2FMR en SPSS: Comparación de efectos simples
- El tercer contraste es la diferencia en el efecto de A cuando está presente \(b_2\) en comparación con la presencia de \(b_3\). Para determinar la significación de esta comparación el procedimiento es el mismo que en los casos anteriores. Los resultados de este tercer contraste serían:
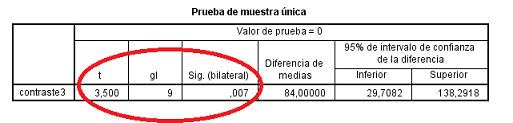
Figura 5.24: Modelo A2FMR en SPSS: Comparación de efectos simples
5.3.1.2 Efectos simples con el programa SPSS
El programa SPSS presenta una tabla donde aparecen las comparaciones entre los distintos efectos simples:
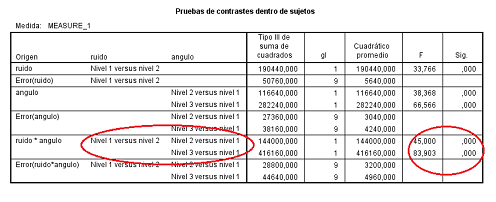
Figura 5.25: Modelo A2FMR en SPSS: Comparación de efectos simples
En la tabla se comparan los efectos simples de A en los niveles 2 y 3 de B con respecto al nivel 1 de B. Ambos resultan ser significativos. Sólo falta la comparación del nivel 3 con el 2. Este se consigue en la ventana de contrastes marcando en vez de la primera categoría, la última:
Figura 5.26: Modelo A2FMR en SPSS: Comparación de efectos simples
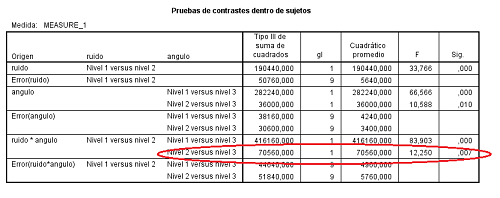
Figura 5.27: Modelo A2FMR en SPSS: Comparación de efectos simples
Vemos que también los resultados son significativos para esta tercera comparación. Asimismo, puede comprobarse que el valor de los estadísticos es igual, ya que el estadístico F es equivalente al estadístico t elevado al cuadrado. Así, en el contraste del nivel 2 con el nivel 3 el estadístico F vale 12,25 y el valor de \(t^2\) = \(3.5^2\) = 12.25.
5.3.1.3 Estudio de los efectos principales
En el caso de que el efecto de la interacción no sea significativo este diseño también permite estudiar los efectos principales. Para ello, se aplica el mismo procedimiento que el utilizado cuando se estudiaron los diseños de medidas repetidas con 1 factor. Así, compararemos las diferencias entre las medias (varianza del tratamiento A o B) con su correspondiente término de error (interacción SxA en el caso de la VI A e interacción SxB en el caso de la VI B). Si estos contrastes resultan significativos habrá que continuar para determinar la significación entre las distintas condiciones. Esto puede hacerse con el procedimiento estudiado anteriormente en el programa SPSS (opción de Contrastes + Comparaciones simples), en el caso de que se cumpla el supuesto de la esfericidad. Si no se cumple este supuestos, pueden realizarse comparaciones dos a dos corrigiendo el nivel de riesgo con el criterio de Bonferroni.
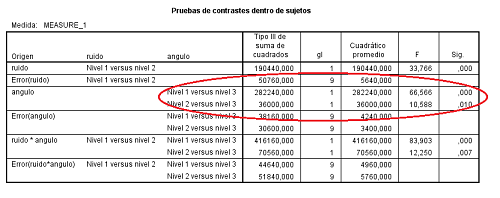
Figura 5.28: Modelo A2FMR en SPSS: Comparación de efectos simples
5.3.2 Análisis del ejemplo 5.2 con SPSS
Un resumen de las distintas condiciones en el diseños son las siguientes:
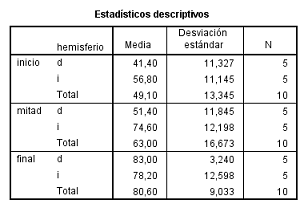
Figura 5.29: Descriptivos
Para realizar el análisis de este tipo de diseños mediante el programa SPSS se utiliza el mismo procedimiento que en los diseños anteriores: Analizar + Modelo lineal general + Medidas repetidas. La única diferencia es que en este caso al introducir las variables es necesario incluir el factor entresujetos tal y como aparece en la siguiente figura:
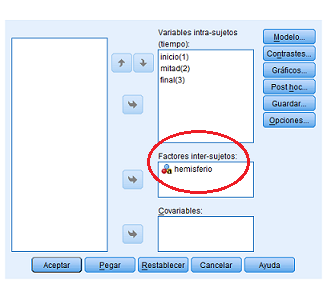
Figura 5.30: Modelo A2FMR en SPSS: Datos del ejemplo 5.2
Los resultados de este ejemplo indican la existencia de una interacción significativa:
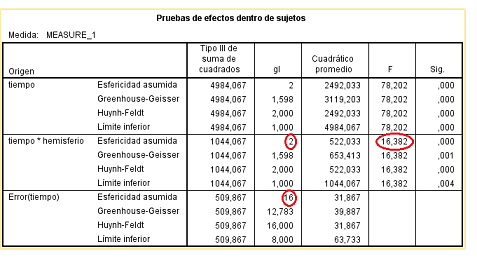
Figura 5.31: Modelo A2FMR en SPSS: Resultados del ejemplo 2
Para considerar como válidos estos resultados es necesario que se cumplan los supuestos del modelo (normalidad, homogeneidad de varianzas-covarianzas y esfericidad). En relación con el supuesto de esfericidad la prueba de Mauchly confirma su existencia:

Figura 5.32: Modelo A2FMR en SPSS: Prueba de esfericidad del ejemplo 2
La prueba de Box-Cox nos permite contrastar el supuesto de homogeneidad de varianzas-covarianzas. Esta prueba se obtiene dentro de la ventana de opciones marcando la opción de pruebas de homogeneidad. Observamos que p = 0.05 por lo que aceptamos la hipótesis de que las matrices de varianzas y covarianzas del grupo con lesión en hemisferio izquierdo es semejante a la del hemisferio izquierdo.

Figura 5.33: Modelo A2FMR en SPSS: Prueba de boxcox del ejemplo 5.2
Encontramos que la comparación entre el efecto simple del nivel 1 frente al 3 muestran diferencias significativas. Para encontrar la comparación entre el nivel 2 y el nivel 3 solo basta cambiar la categoría de referencia (hay que poner la última) en la opción de contrastes. También resulta significativa.
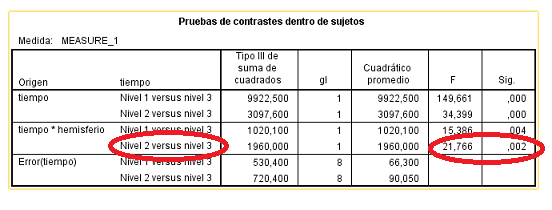
Figura 5.34: Modelo A2FMR en SPSS: Comparación de los efectos simples