1.5 Contrastes de hipótesis en los programas estadísticos
1.5.1 Contrastes para 1 variable
El árbol de decisión para estos contrastes es el siguiente:
Figura 1.3: Contrastes para 1 variable
1.5.1.1 Prueba t para 1 muestra mediante el programa JAMOVI
Se selecciona el módulo de “Pruebas T” y marcamos la opción ”Prueba T para una muestra”. En la ventana de la prueba T para una muestra aparece por defecto seleccionada la prueba T y marcando la opción de “Comprobación de supuestos” puede obtenerse el resultado de la prueba de normalidad. Para realizar el análisis es necesario indicar el valor de prueba en la sección de “Hipótesis” (en nuestro ejemplo se ha introducido el valor de 47). Por defecto, aparece marcada la opción del contraste bilateral aunque existen opciones para estudiar los contrastes unilaterales. Asimismo, tendríamos que marcar la opción de “Rangos de Wilcoxon” en el caso de que no se acepte la hipótesis de normalidad.
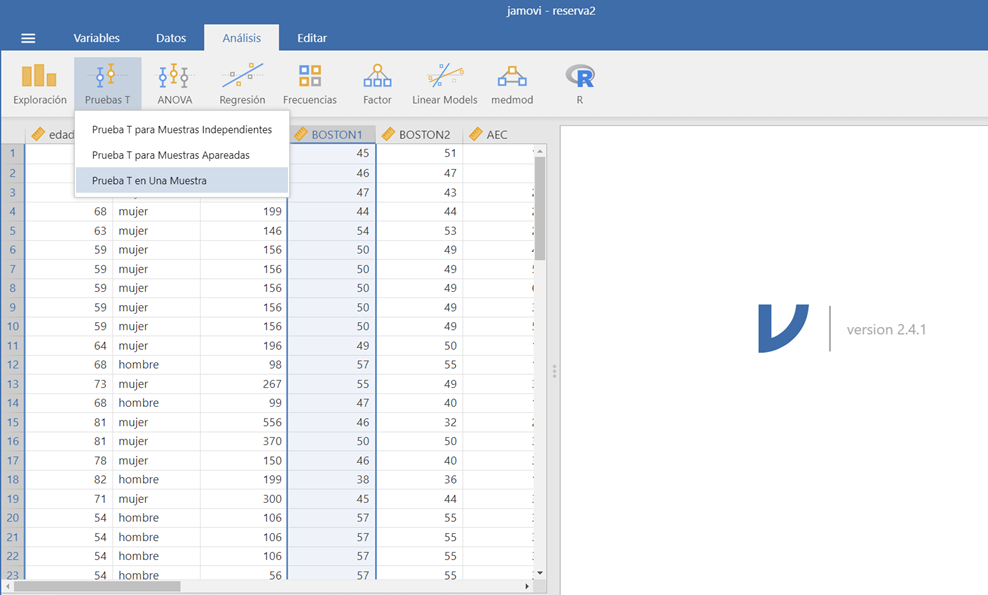
Figura 1.4: Prueba t para una muestra en JAMOVI
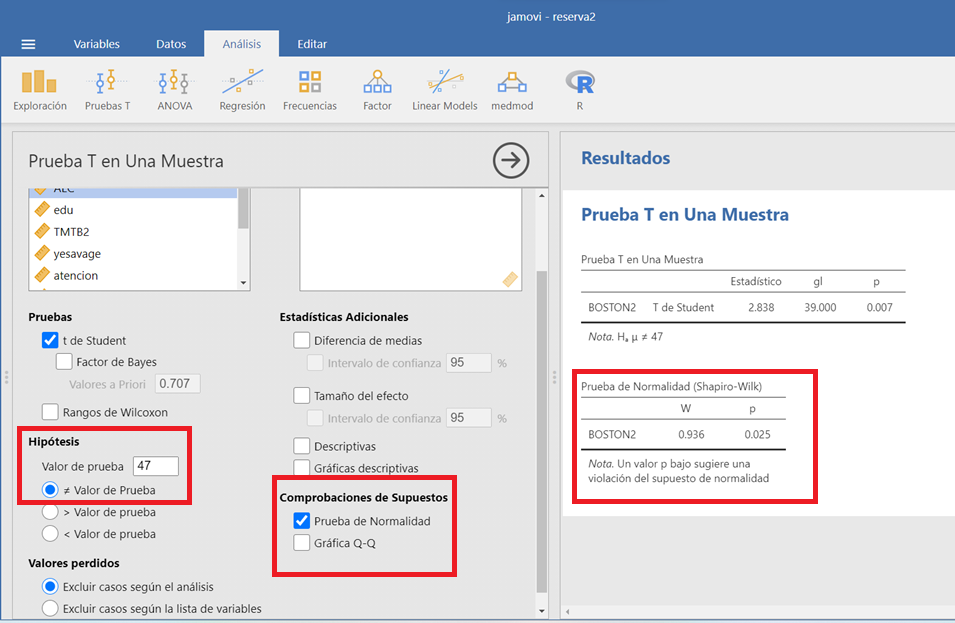
Figura 1.5: Prueba t para una muestra en JAMOVI
1.5.1.2 Prueba t para 1 muestra en el programa SPSS
1.5.1.2.1 Prueba de normalidad de Shapiro-Wilk
Para determinar la normalidad será necesario aplicar la prueba de Shapiro-Wilk. En el programa SPSS se hace marcando Analizar + Explorar + Gráficos + Gráficos con pruebas de normalidad. Los resultados obtenidos pueden observarse en las siguientes imágenes.
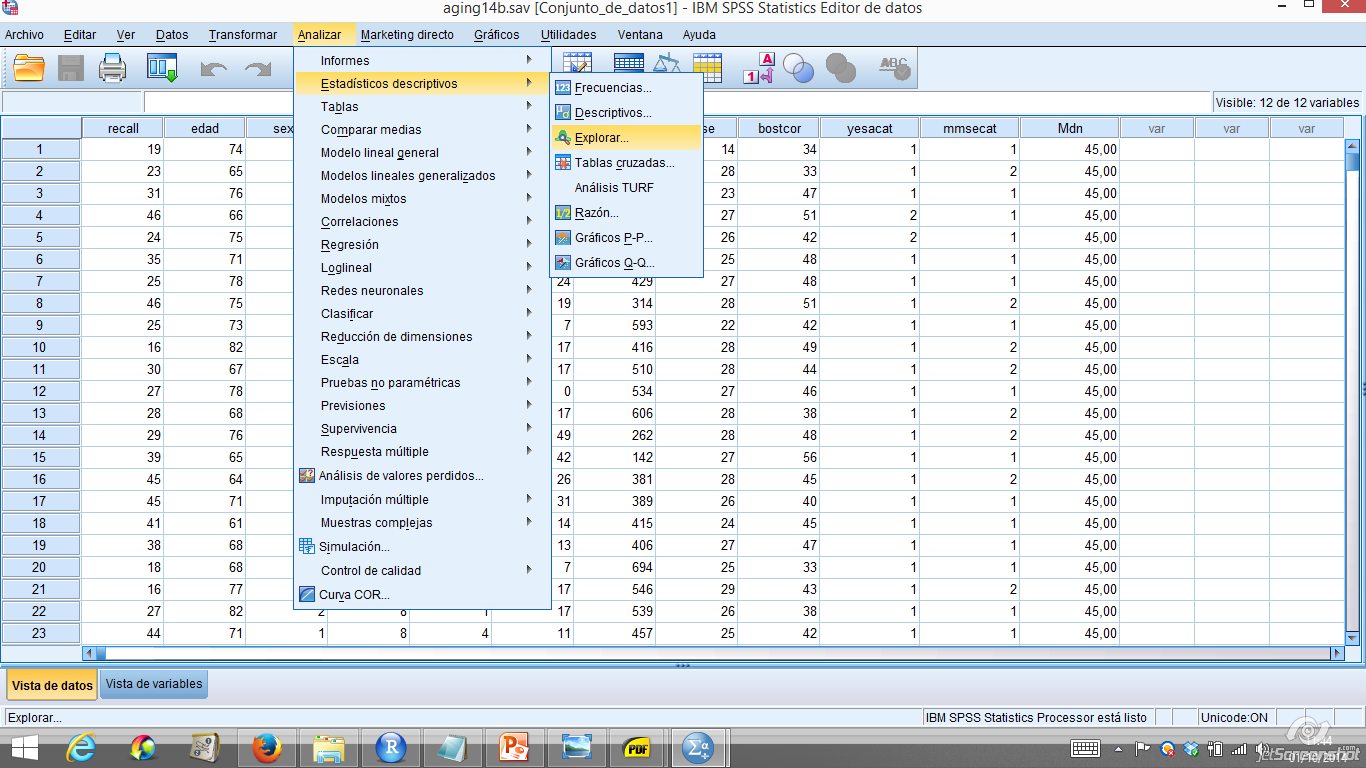
Figura 1.6: Prueba de normalidad Shapiro-Wilk en el programa SPSS
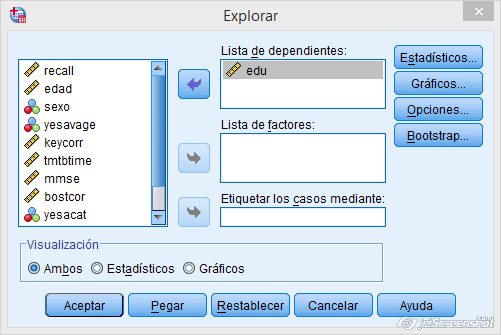
Figura 1.7: Prueba de normalidad en SPSS
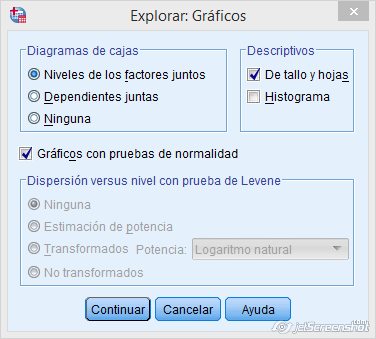
Figura 1.8: Prueba de normalidad en SPSS

Figura 1.9: Resultados de la prueba de normalidad
La prueba t para 1 muestra se realiza marcando Analizar + Comparar medias + Prueba T para una muestra:
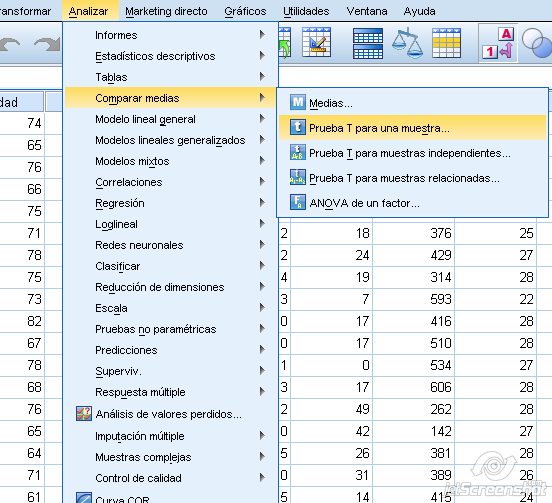
Figura 1.10: Prueba t para una muestra en el programa SPSS
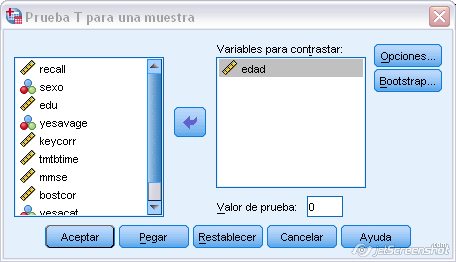
Figura 1.11: Prueba t para una muestra en el programa SPSS
Será necesario introducir la VD a estudiar en el cuadro de “Variable a contrastar”. El valor del contraste es cero por defecto, pero habrá que introducir el valor de la hipótesis a estudiar.
1.5.1.2.2 Prueba de Wilcoxon para una muestra
Necesitamos marcar Analizar + Pruebas no paramétricas + Cuadro de diálogos antiguos + 2 muestras relacionadas. Observamos que el programa SPSS nos pide introducir dos variables, ya que esta prueba está diseñada para estudiar la relación entre dos variables. Sin embargo, puede utilizarse introduciendo la variable en cuestión y como segunda variable una nueva que hemos creado con el valor de contraste de nuestras hipótesis (en la figura aparece con el nombre de Mdn):
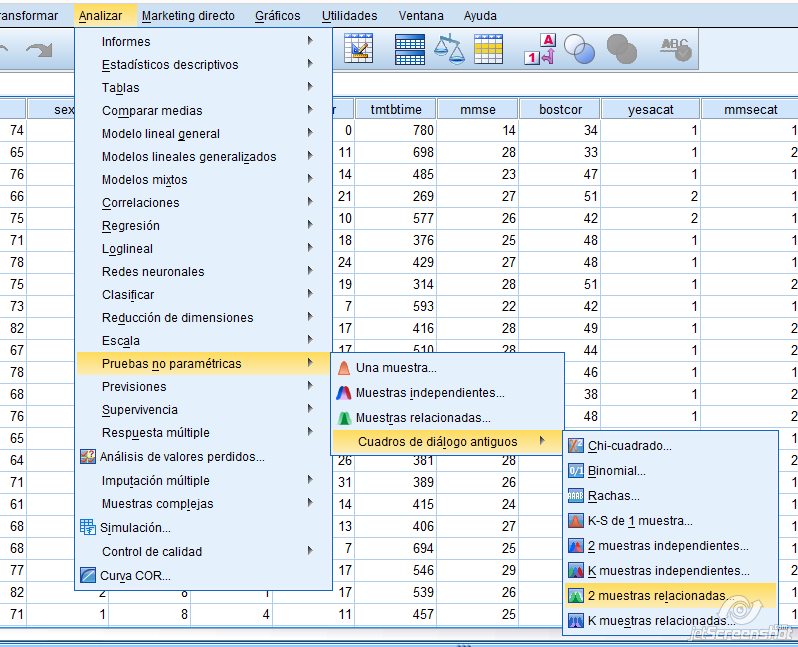
Figura 1.12: Prueba de Wilcoxon en el SPSS
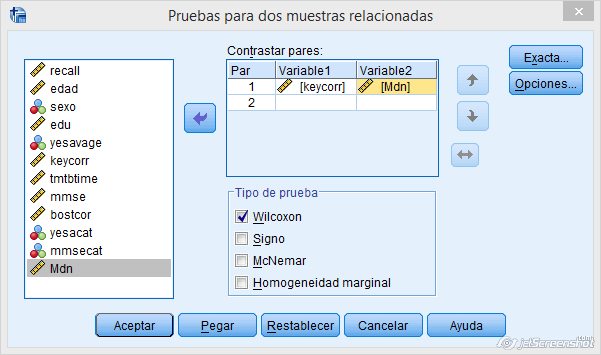
Figura 1.13: Prueba de Wilcoxon en el SPSS
1.5.2 Contrastes para 1 VI cualitativa y una VD cuantitativa
El árbol de decisión para los diseños en los que solo hay 1 medida por sujeto (muestras independientes) es:
Figura 1.14: Técnicas para dos muestras independientes
1.5.2.1 Prueba t para muestras independientes en JAMOVI
Se selecciona la opción de muestras independientes en el modulo de “Pruebas T”. Se introduce la variable dependiente (cuantitativa) en el cuadro de “Variables dependientes” y la variable cualitativa en el cuadro de “Variable de agrupación”. Se seleccionan las opciones para comprobar los supuestos de la prueba y se elige la prueba (T de student, T de Welch o U de Mann-Whitney), dependiendo de los supuestos que se cumplan.
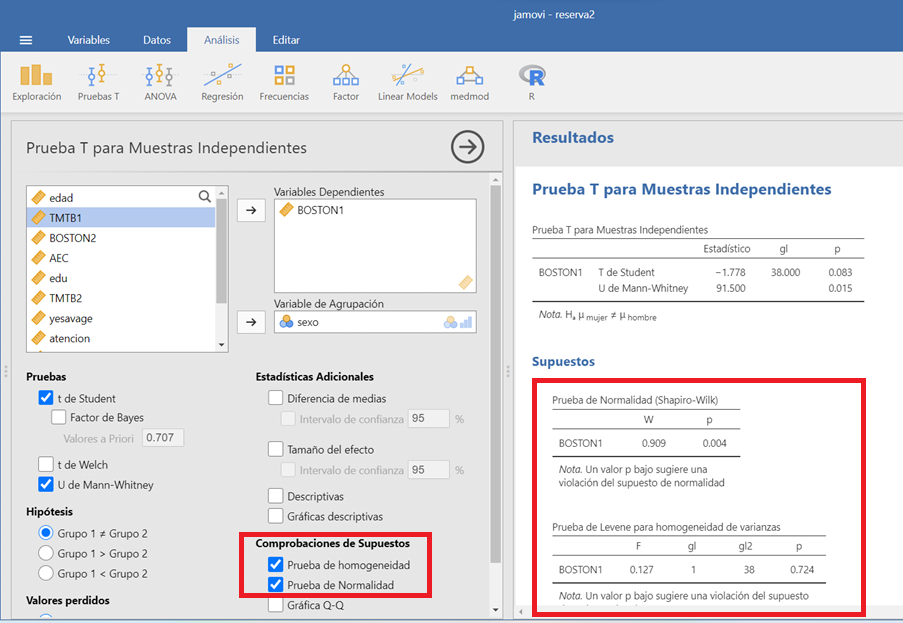
Figura 1.15: Prueba t para muestras independientes en JAMOVI
1.5.2.2 Prueba t para muestras independientes en SPSS
Se realiza marcando Analizar + Comparar medias + Prueba T para muestras independientes:
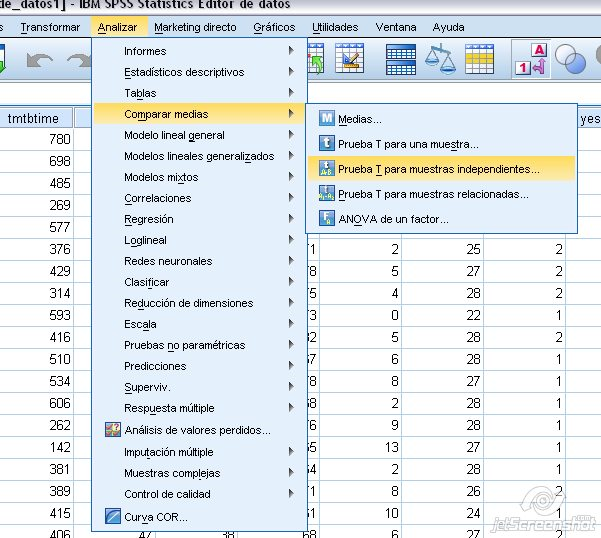
Figura 1.16: Prueba t para muestras independientes en SPSS
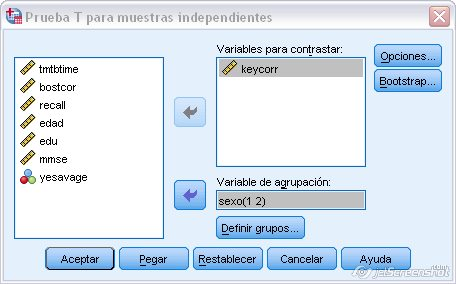
Figura 1.17: Prueba t para muestras independientes en SPSS
1.5.2.3 Prueba U de Mann-Whitney para muestras independientes en SPSS
Se obtiene marcando Analizar + Pruebas no paramétricas + Cuadro de diálogos antiguos + 2 muestras independientes.
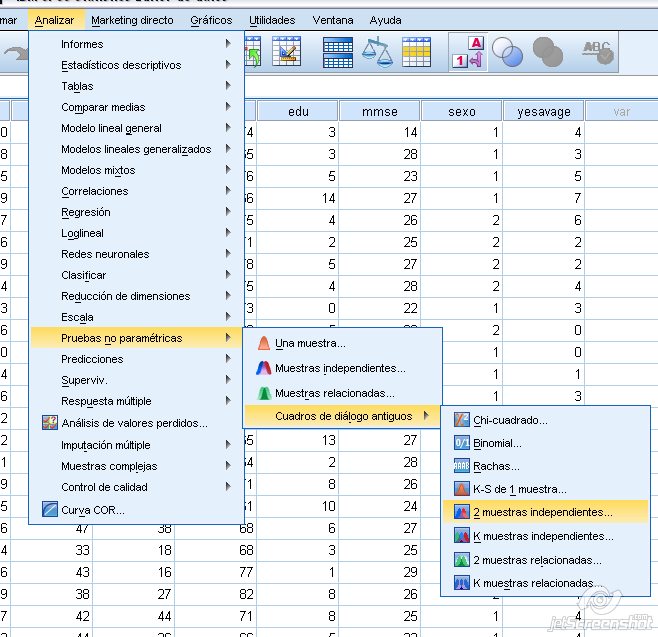
Figura 1.18: Prueba U para muestras independientes en SPSS
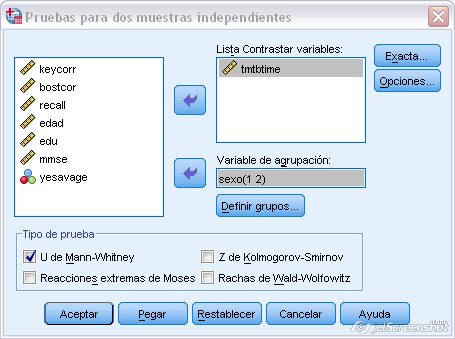
Figura 1.19: Prueba U para muestras independientes en SPSS
1.5.3 Pruebas para muestras relacionadas (2 medidas por unidad de observación)
El árbol de decisión para este apartado es el siguiente:
Figura 1.20: Pruebas para dos muestras relacionadas
La variable sobre la que se realiza el contraste es la diferencia entre las medidas de los dos momentos. Por tanto, el análisis de estos diseños se convierte en el análisis sobre 1 muestra que ya se ha estudiado anteriormente.
1.5.3.1 Prueba t para muestras relacionadas en el programa JAMOVI
Se selecciona la opción de “Muestras Apareadas” en el modulo de “Pruebas T”. Se introduce las dos variables dependientes (cuantitativas) en el cuadro de *“Variables Apareadas”. Se selecciona la opción “Comprobación de supuestos” de la prueba y se elige la prueba (T de student o W de Wilcoxon), dependiendo de que se cumpla el supuesto de normalidad. Estos resultados son los mismos que si se hubieran calculado la diferencia entre las dos medidas y se hubiera aplicado la prueba T para una muestra.
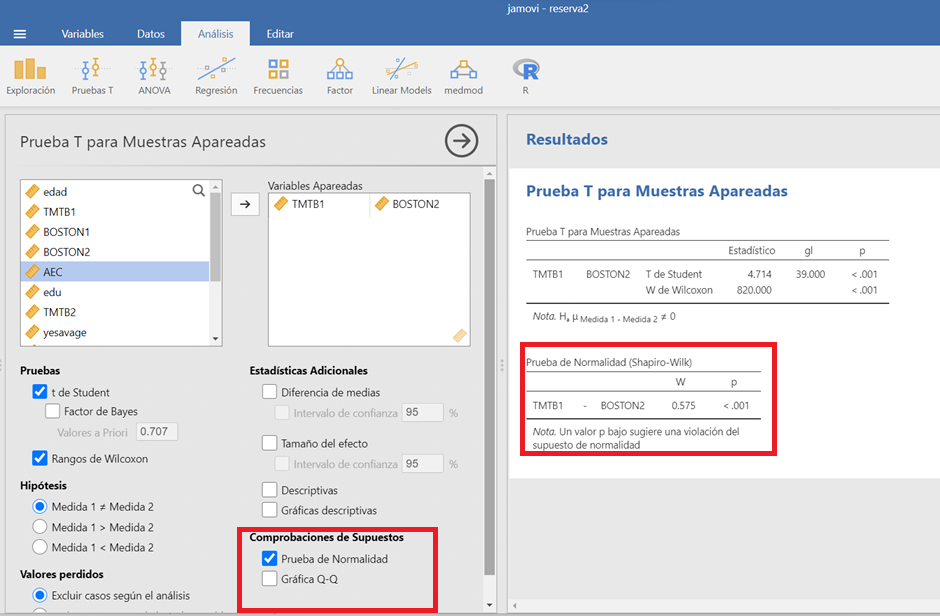
Figura 1.21: Prueba t para muestras relacionadas en JAMOVI
1.5.3.2 Prueba t para muestras relacionadas en el programa SPSS
Se realiza marcando Analizar + Comparar medias + Prueba T para muestras relacionadas:
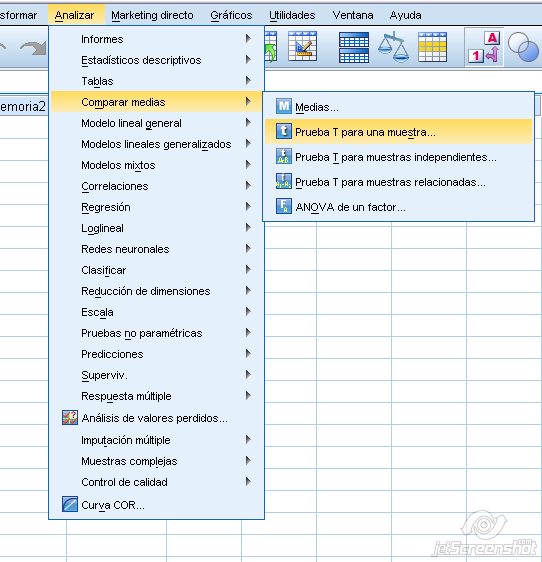
Figura 1.22: Prueba t para muestras relacionadas en SPSS
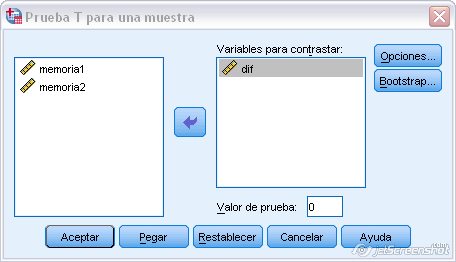
Figura 1.23: Prueba t para muestras relacionadas en SPSS
1.5.3.2.1 Prueba de Wilcoxon para 2 muestras relacionadas
Necesitamos marcar Analizar + Pruebas no paramétricas + Cuadro de diálogos antiguos + 2 muestras relacionadas.
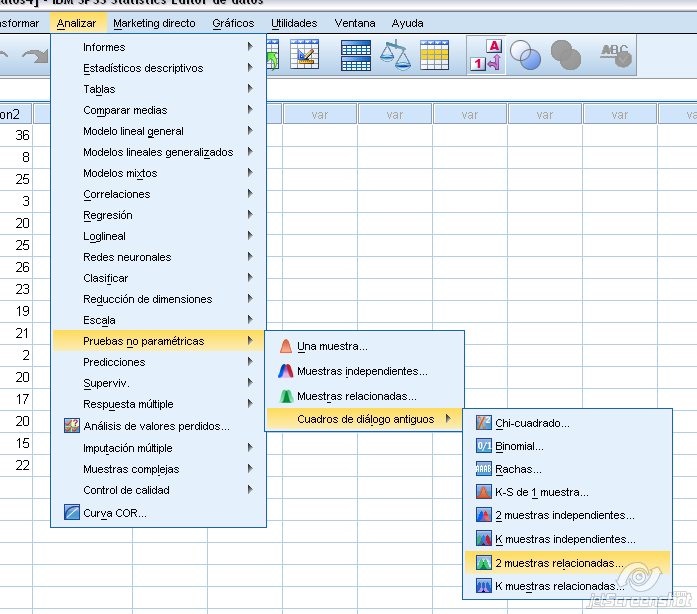
Figura 1.24: Prueba de Wilcoxon para muestras relacionadas en SPSS
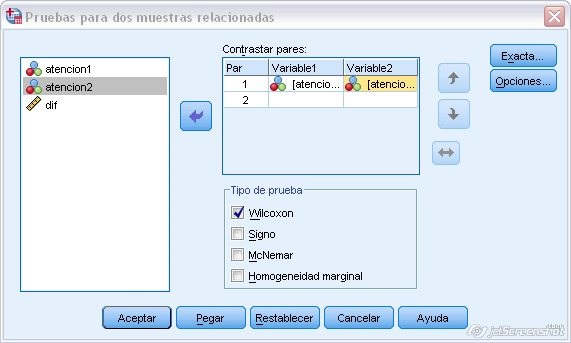
Figura 1.25: Prueba de Wilcoxon para muestras relacionadas en SPSS