1.2 Validez de las investigaciones
La validez de un estudio depende la naturaleza de las variables y sus definiciones, del diseño de investigación y de la técnica estadística utilizada.
1.2.1 Validez de las variables y definiciones
En toda investigación científica se trabaja con conceptos que deben ser operacionalizados para que puedan ser medidos y presenten un significado unívoco. Los problemas de validez surgen cuando las operaciones realizadas no tienen nada que ver con el constructo estudiado o su vinculación es parcial.
Las variables pueden medirse mediante cuatro escalas de medida (nominal, ordinal, intervalo y razón). La elección del tipo de medida determinará el tipo de análisis de los datos. Hay ocasiones en las que se han utilizado los términos de cualitativo y cuantitativo para clasificar los distintos tipos de variables (Ato & Vallejo, 2007). Dentro de las variables cualitativas suelen diferenciarse las variables en función de que su escala de medida sea nominal u ordinal. Las variables cuantitativas se distinguen en función de que su dominio sea discreto o continuo.
Otra clasificación frecuente en Psicología es la distinción entre variable independiente (VI) o variable predictora (VP), variable dependiente (VD) y variables extrañas (VVEE). En ocasiones se se denomina a la VD variable criterio en los contextos en los que no hay manipulación en el diseño de investigación. En estos estudios a la VD también se le denomina variable de respuesta (VR) y a la VI variable predictora.
1.2.2 Validez del diseño de investigación
Con el diseño tenemos que asegurarnos de que las variables extrañas están debidamente controladas (validez interna). Para ello, resulta conveniente utilizar técnicas de control tales como la manipulación de la VI, la aleatorización, el mantenimiento constante de dichas variables o el control estadístico. Asimismo, es importante considerar la generalización de los resultados del estudio a otras situaciones. En este caso, estamos hablando de validez externa.
1.2.3 Validez de conclusión estadística
La elección de la técnica estadística también influye en la validez de la investigación. Una técnica mal seleccionada puede llevarnos a sacar conclusiones inadecuadas. Afecta a la determinación de la existencia de covariación entre las variables y a su grado. El procedimiento para obtener conclusiones estadísticas es el contraste de hipótesis. Este procedimiento consiste en la toma de decisiones sobre dos hipótesis rivales y excluyentes en base a la probabilidad calculada de un estadístico. Más adelante se desarrollará este concepto para su completa comprensión.
Entre los errores que se cometen mediante la contrastación de hipótesis es el considerar que existe relación cuando no existe (error tipo I o riesgo \(\alpha\)), o considerar que no existe relación cuando la hay (error tipo II o riesgo \(\beta\)). Otro error posible es la sobre-estimación o infra-estimación de la relación. Posibles factores que pueden afectar a la conclusión estadística es la baja potencia y la violación de los supuestos. También es importante considerar la magnitud del efecto y la significación práctica y clínica de los resultados.
1.2.4 Contraste de hipótesis estadísticas
Dentro de la inferencia estadística buscamos realizar comparaciones y establecer relaciones mediante la estimación de parámetros y el contraste de hipótesis. El primer procedimiento puede hacerse mediante la estimación puntual o por intervalos. En cambio, el contraste de hipótesis es la toma de decisiones acerca de si un conjunto de datos corrobora una hipótesis. Supone cubrir una serie de etapas:
1) Formulación de las hipótesis: Se plantean la hipótesis nula (\(H_0\)) que considera que las variaciones existentes entre las condiciones se debe al azar y la hipótesis alternativa (\(H_1\)) que niega la hipótesis nula y considera que las variaciones en una variable están relacionadas con los cambios en la otra. Las hipótesis pueden ser bidireccionales (no conocemos el sentido de la relación como por ejemplo \(\mu_1 = \mu_2\)) o unidireccionales (el investigador plantea donde se encontrarán las diferencias como por ejemplo \(\mu_1 \leq \mu_2\) ).
2) Definición del estadístico de contraste: Su cálculo supone la realización de un estudio empírico en el que se ha extraído una muestra aleatoria de la población. Este estadístico debe tener una distribución de probabilidad conocida.
3) Regla de decisión: Se basa en la compatibilidad que existe entre la hipótesis nula y los datos empíricos (Pardo & San Martin, 2010). Permite determinar la probabilidad de que \(H_0\) sea cierta en base a nuestros resultados. Para determinar el grado de apoyo de \(H_0\) se divide a la distribución teórica en dos regiones (región de confianza y región crítica). La región de confianza es la zona de la distribución teórica en la que se acepta \(H_0\). Existe consenso en considerar que esta región alcance el 95% de probabilidad. La región crítica es la zona complementaria a la región de confianza (por lo que cubre el 5% de la distribución) y si el estadístico pertenece a esa zona se rechaza \(H_0\). Si la hipótesis es bilateral la región crítica estará a ambos lados de la distribución teórica. En cambio, si la hipótesis es unilateral la región de confianza estará situada en una de las colas de las distribución.
Ejemplo 1.1: A continuación, se presentan los resultados de un estudio en el que se quiso comparar el aprendizaje de los niños dependiendo del tipo de método (fonético versus global). Cada niño sólo fue entrenado con un único método y se quería conocer si había diferencias significativas entre ambos métodos. Nos estamos planteando una hipótesis bidireccional:
| Fonetico | 6 | 6 | 3 | 4 | 2 | 5 | 7 |
| Global | 4 | 5 | 6 | 7 | 8 | 4 | 8 |
- \(H_0\): No hay diferencias entre los métodos de aprendizaje (\(\mu_{F} = \mu_G\))
- \(H_1\): El aprendizaje depende del método (\(\mu_{F} \neq \mu_G\))
Para contrastar esta hipótesis necesitamos un estadístico con distribución de probabilidad conocida. En este caso, es el estadístico t de Student:
\[ \bar{Y}_{\bar{Y}_{1} - \bar{Y}_{2}}= \bar{Y}_{1} - \bar{Y}_{2} \]
\[ Var(\bar{Y}_{1} - \bar{Y}_{2}) = \sigma_{1}^{2}/n_{1} + \sigma_{2}^{2}/n_{2} \]
\[ t = \frac{\bar{Y}_{\bar{Y}_{1} - \bar{Y}_{2}}}{Var(\bar{Y}_{1} - \bar{Y}_{2})} \sim t(n-2) \] En nuestro ejemplo, el valor del estadístico t puede obtenerse con el programa R:
##
## Two Sample t-test
##
## data: rendimiento by metodo
## t = -2.5955, df = 12, p-value = 0.02342
## alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
## 95 percent confidence interval:
## -4.2044435 -0.3669851
## sample estimates:
## mean in group 1 mean in group 2
## 4.142857 6.428571Encontramos que el valor del estadístico t vale -2.596 y su valor de probabilidad es 0.023. En base a estos resultados podemos rechazar \(H_0\). Esto significa que el estadístico t se aleja bastante de la predicción establecida mediante la hipótesis nula. Es decir, existe muy poca compatibilidad entre nuestros datos y \(H_0\).
Para aceptar estos resultados debemos confirmar que se cumplen los supuestos de la prueba (normalidad de las muestras y homogeneidad de las varianzas 1):
##
## Shapiro-Wilk normality test
##
## data: rendimiento[1:7]
## W = 0.92025, p-value = 0.4713##
## Shapiro-Wilk normality test
##
## data: rendimiento[8:14]
## W = 0.91511, p-value = 0.4324| Df | F value | Pr(>F) | |
|---|---|---|---|
| group | 1 | 0.06 | 0.8106346 |
| 12 | NA | NA |
Ejemplo 1.2: A continuación, se presentan los resultados de un estudio en el que se quiso comparar el aprendizaje de los niños dependiendo del tipo de método (fonético versus global). Cada niño sólo fue entrenado con un único método y se esperaba encontrar un mayor rendimiento con el método global. Aquí nos planteamos una hipótesis unidireccional:
| Fonetico | 6 | 6 | 3 | 4 | 2 | 5 | 7 |
| Global | 4 | 5 | 6 | 7 | 8 | 4 | 8 |
- \(H_0\): No hay diferencias en el aprendizaje (\(\mu_{F} \geq \mu_G\))
- \(H_1\): El aprendizaje es mejor con el método global (\(\mu_{F} < \mu_G\))
Para contrastar esta hipótesis necesitamos un estadístico con distribución de probabilidad conocida. En este caso, el estadístico es el mismo y tiene el mismo valor. Sólo cambia su probabilidad:
##
## Two Sample t-test
##
## data: rendimiento by metodo
## t = -2.5955, df = 12, p-value = 0.01171
## alternative hypothesis: true difference in means between group 1 and group 2 is less than 0
## 95 percent confidence interval:
## -Inf -0.7161774
## sample estimates:
## mean in group 1 mean in group 2
## 4.142857 6.428571Ejemplo 1.3: Con los mismos datos del ejemplo anterior supongamos que el investigador está interesado en conocer si la media del rendimiento en la población de los estudiantes es 6. Para ello formula las siguientes hipótesis:
- \(H_0\): \(\mu_{rendimiento}\) = 6
- \(H_1\): \(\mu_{rendimiento} \neq\) 6
Como no conocemos el sentido de la dirección asumimos que la hipótesis es bilateral. Para contrastar esta hipótesis necesitamos conocer si la distribución de la variable sigue una ley normal. En caso de que se cumpla esta hipótesis realizaremos el contraste con la prueba t para una muestra. Si no se cumple, usaremos la prueba de Wilcoxon para una muestra. El estadístico de Shapiro-Wilk indica que se cumple la normalidad de la variable por lo que usamos la prueba t.
##
## Shapiro-Wilk normality test
##
## data: rendimiento
## W = 0.92677, p-value = 0.2747##
## One Sample t-test
##
## data: rendimiento
## t = -1.3512, df = 13, p-value = 0.1997
## alternative hypothesis: true mean is not equal to 6
## 95 percent confidence interval:
## 4.143709 6.427720
## sample estimates:
## mean of x
## 5.285714Aceptamos la hipótesis de que el valor medio de la variable rendimiento es 6 en la población.
Ejemplo 1.4: Supongamos que construimos un examen para evaluar los conocimientos de los estudiantes de Psicología en la materia de Diseño y Análisis de Datos II. El examen tendrá 10 preguntas con 3 opciones de respuesta y solo una correcta. Queremos conocer cuántas preguntas debe responder correctamente el alumno para estar seguros de que domina la materia y de que no ha respondido por azar. Las hipótesis en este contraste estadístico serán:
- \(H_0\): El alumno no sabe por lo que responde al azar (\(\pi_{acierto} \leq\) 0.333)
- \(H_1\): El alumno sabe. No responde al azar (\(\pi_{acierto} >\) 0.333)
Ahora necesitamos determinar cuántas preguntas suponen responder por azar. Está claro si el alumno acierta sólo 1 pregunta la probabilidad de que haya respondido por azar 0 ó 1 es muy alta. En la siguiente figura se aprecia que los valores más probables están comprendidos entre 2 y 4:
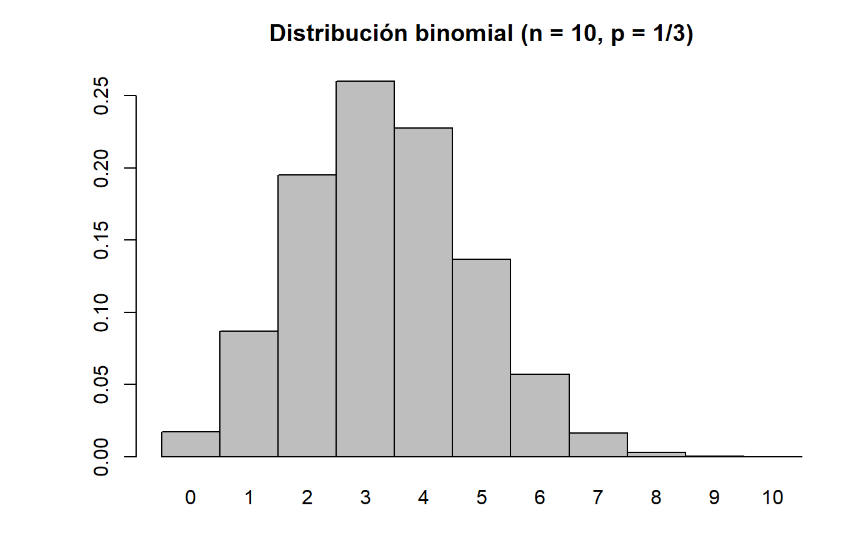
Figura 1.1: Distribución binomial
## [1] 0.1950922## [1] 0.2601229## [1] 0.2276076Por tanto, necesitamos encontrar el número de preguntas acertadas que tengan una probabilidad de ser acertadas por azar \(\leq\) 0,05. Esto se consigue con 6 preguntas acertadas. Con 5 preguntas acertadas estaríamos por encima del nivel de riesgo establecido por convención del 5%:
[1] 0.9803384
[1] 0.01966164
[1] 0.07656353
No obstante, el criterio de 0,05 es un criterio establecido arbitrariamente y que supone la ausencia de factores contaminantes que estarían actuando en la situación real de examen y que podrían afectar al resultado del examen. Un profesor algo más exigente podría considerar la necesidad de aprobar acertando 7 preguntas. En este caso, la probabilidad de que un estudiante acertara por azar sería:
[1] 0.996596
[1] 0.003403953
En este caso no es necesario calcular la normalidad de los errores, ya que si las muestras son normales también serán normales los errores. Esto se verá con más claridad en el próximo tema.↩︎