5.1 Diseño factorial intrasujeto

Presentamos primero el caso en el que los dos factores son estudiados mediante la estrategia del sujeto como propio control (medidas repetidas). Su modelo estadístico es:

\[ Y_{ijk} =\mu+\alpha_i+\beta_j+ \pi_k + (\alpha\beta)_{jk}+ (\alpha\pi)_{ji}+ (\beta\pi)_{ki}+(\alpha\beta\pi)_{jki}+\epsilon_{ijk} \left\{\begin{array}{ccrccr} i&=& 1,&2,&\dots,&n \\ j &=&1,&2,&\dots,&a \\ k &=&1,&2,&\dots,&b \\ \end{array}\right. \]

donde \(Y_{ijk}\) es la medida de la VD del sujeto i en la condición jk; \(\mu\) es una constante (la media global de todas las puntuaciones); \(\alpha_j\) es el efecto del tratamiento \(a_j\); \(\beta_k\) es el efecto del tratamiento \(b_k\); \(\pi_i\) es el efecto asociado al sujeto i; \((\alpha\beta)_{jk}\) es el efecto de la combinación de tratamientos \(a_jb_k\); \((\alpha\pi)_{ji}\) es el efecto de la interacción entre el tratamiento j del factor A y el sujeto i; \((\beta\pi)_{ji}\) es el efecto de la interacción entre el tratamiento k del factor B y el sujeto i; \((\alpha\beta\pi)_{jki}\) es el efecto de la interacción de tercer orden del nivel j del factor A, el k-ésimo nivel del factor B y el i-ésimo sujeto. Por último, \(\epsilon_{ijk}\) es el término del error.

Al igual que en otros modelos de ANOVA factoriales, el investigador está interesado en estudiar los efectos principales y de interacción. Cada uno de estos efectos se realiza mediante la prueba F donde se comparan las medias cuadráticas de cada uno de los efectos con sus correspondientes medias cuadráticas del error.

5.1.1 Ejemplo 1: Diseño factorial de medidas repetidas

Un ejemplo de este tipo de diseños propuesto por Maxwell & Delaney (2004) en el que se deseaba estudiar el efecto de la presencia de distractores (ruido o sin ruido) y la orientación del estímulo (0 , 4 y 8 grados) en una prueba de percepción donde se pretende discriminar entre dos estímulos. La VD fue el tiempo de reacción. Los resultados aparecen en la siguiente tabla:

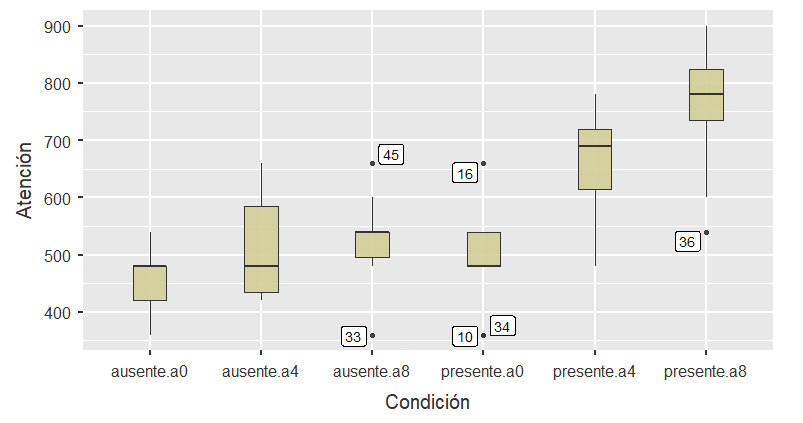
Figura 5.1: Modelo AF2MR: Boxplot del ejemplo 5.1

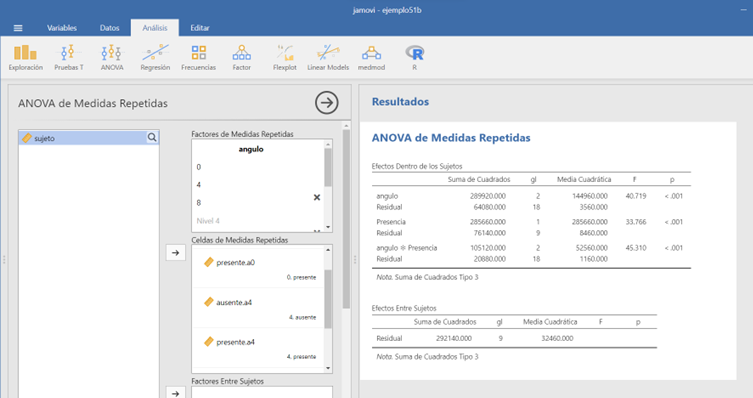
Figura 5.2: Modelo AF2MR: Resultados del ejemplo 5.1

Estos resultados son válidos siempre y cuando se cumpla el supuesto de esfericidad estudiado en el tema 3. Una vez comprobado este supuesto con la prueba de Mauchly pueden tomarse decisiones acerca de la significación de los efectos. En este ejemplo la prueba de esfericidad nos permite aceptar la hipótesis nula. Asimismo, se puede observar que los valores de \(\epsilon\) de Geisser-Greenhouse (GG) son más pequeños que los de Huynh-Feldt (HF). Utilizar los valores de GG para realizar los contrastes de hipótesis supone aplicar una estrategia conservadora en el análisis de los datos.

Figura 5.3: Modelo A2FMR: Prueba de esfericidad del ejemplo 5.1

5.1.1.1 Tamaño del efecto

Aunque puede utilizarse el estadístico \(\eta^2\) para determinar el tamaño del efecto, los autores prefieren estimar este estadístico mediante \(\omega^2\). En este tipo de diseños la fórmula para calcularlo es:

• Para el efecto A (ruido):

\[ \omega_{A}^2 = \frac{(a-1)(F_A - 1)}{(a-1)(F_A - 1)+ nab} = \frac{1*(33.766 - 1)}{1*(33.766 - 1) + 10*2*3} = 0.353 \]

• Para el efecto B:

\[ \omega_{B}^2 = \frac{(b-1)(F_B - 1)}{(b-1)(F_B - 1)+ nab} = \frac{(3-1)*(40.719 - 1)}{(3-1)*(40.719 - 1) + 10*2*3} = 0.569 \]

• Para el efecto AB:

\[ \omega_{AB}^2 = \frac{(a-1)(b-1)(F_{AB} - 1)}{(a-1)(b-1)(F_{AB} - 1)+ nab} = \frac{(3-1)*(45.310 - 1)}{(3-1)*(45.310 - 1) + 10*2*3} = 0.596 \]

Si hubiéramos utilizado el estadístico \(\eta^2\) proporcionado por el programa SPSS obtendríamos los siguientes valores: 0.79 para el factor A, 0.819 para el factor B y 0.834 para el factor AB. Tal y como señalan Pardo & San Martin (2010) estos valores están bastante inflados y no son un buen estimador del tamaño del efecto. Otra medida de tamaño del efecto equivalente al de \(\omega^{2}\) es la de eta generalizada al cuadrado (\(\eta_g^{2}\)) que utiliza el programa JAMOVI (The Jamovi Team, 2022).

5.1.1.2 Estudio de la interacción

Al igual que se mencionó en el tema 4, para estudiar los efectos interactivos lo que tenemos que hacer es comparar los efectos simples. En este diseño tenemos 3 efectos simples por lo que habrá que realizar tres comparaciones. La primera comparación sería la siguiente:

\[ \phi_1 = \overline{X}_{ausente.a0} - \overline{X}_{presente.a0} - (\overline{X}_{ausente.a4} - (\overline{X}_{presente.a4}) = \overline{X}_{a_1b_1} - \overline{X}_{a_2b_1} - (\overline{X}_{a_1b_2} - \overline{X}_{a_2b_2}) \]

• Para introducir los coeficientes de los contrastes es necesario seguir el orden de las condiciones que aparecen en el fichero de datos. La forma más sencilla de realizar este contraste es creando una nueva variable con la suma de las puntuaciones de las medias que se comparan. En este caso, estamos realizando lo siguiente:

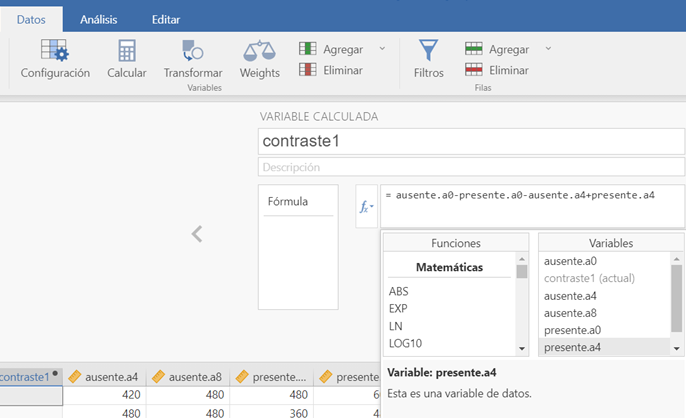
Figura 5.4: Modelo A2FMR en JAMOVI: Comparación efectos simples

Esta nueva variable creada (Contraste 1) supone una combinación lineal (suma de varias puntuaciones correspondientes a 4 variables). Bajo el modelo de hipótesis nula la suma de esta variable debe ser igual a 0. Para contrastar esta hipótesis podemos utiliazar la prueba T para una muestra (o la prueba de Wilcoxon en el caso de que no se cumpla el supuesto de normalidad). Los resultados de este análisis nos indican que rechazamos la hipótesis nula. Es decir existe un efecto interactivo significativo cuando se comparan los efectos simples de A en \(b_1\) y \(b_2\).

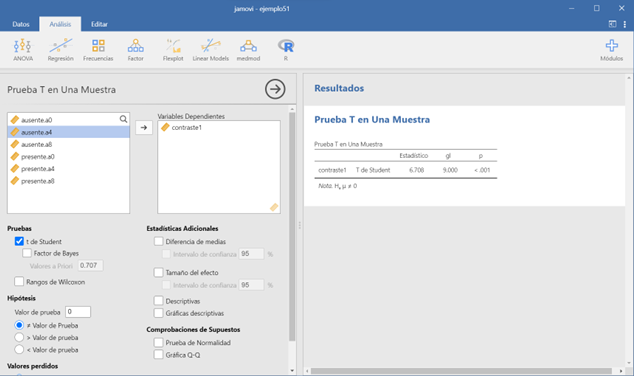
Figura 5.5: Modelo A2FMR en JAMOVI: Resultado de la comparación del efecto de A en \(b_1\) y \(b_2\)

Observamos que el efecto resulta ser significativo de tipo positivo por lo que el efecto de A es distinto en \(b_1\) que en \(b_2\). En concreto, en \(b_1\) el efecto de A vale -30. En cambio, en \(b_2\) el efecto de A vale -150. Esto se aprecia muy bien en la gráfica:

Figura 5.6: Gráfico de medias del ejemplo 5.1

La segunda comparación entre los efectos simples sería la comparación del efecto de A cuando están presentes \(b_1\) y \(b_3\)

\[ \phi_2 = \overline{X}_{ausente.a0} - \overline{X}_{presente.a0} -(\overline{X}_{ausente.a8} - \overline{X}_{presente.a8}) \]

Creamos una nueva variable que denominamos Contraste 2 de la siguiente forma:

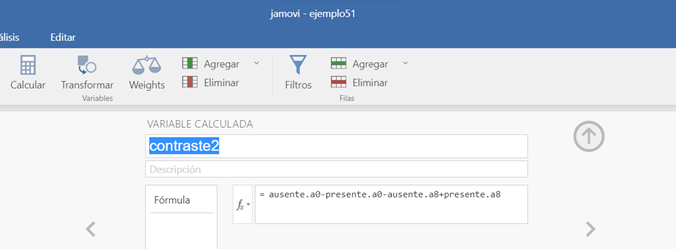
Figura 5.7: Modelo A2FMR en JAMOVI: Comparación de efectos simples

Los resultados obtenidos con este segundo contraste se muestran en la siguiente figura:

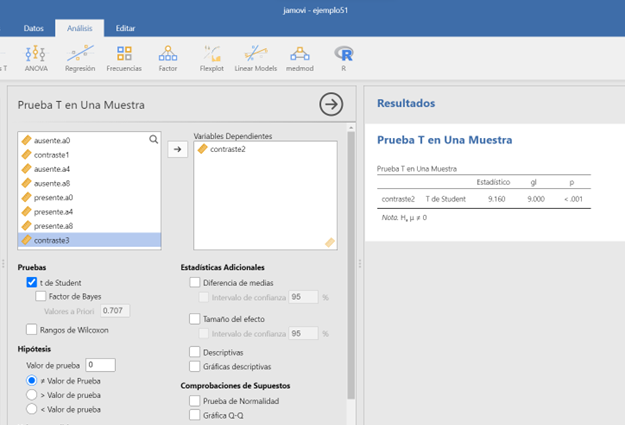
Figura 5.8: Modelo A2FMR en JAMOVI: Comparación de efectos simples

Encontramos de nuevo que el efecto de A en \(b_1\) es mucho menor que cuando está presente \(b_3\). El efecto de A en \(b_1\) vale -30. En cambio, cuando está presente \(b_3\) el valor es -234. Para terminar nos queda ver si existen diferencias en el efecto de A cuando está presente \(b_2\) en comparación con la presencia de \(b_3\). Sabemos que cuando está presente \(b_2\) el efecto de A vale -150, mientras que cuando está presente \(b_3\) vale -234. Para determinar la significación de esta comparación el procedimiento es el mismo que en los casos anteriores. La comparación sería la siguiente:

\[ \phi_3 = \overline{X}_{ausente.a4} - \overline{X}_{presente.a4} - (\overline{X}_{ausente.a8} - (\overline{X}_{presente.a8}) = \overline{X}_{a_1b_2} - \overline{X}_{a_2b_2} - (\overline{X}_{a_1b_3} - \overline{X}_{a_2b_3}) \]

Los resultados de este tercer contraste sería:

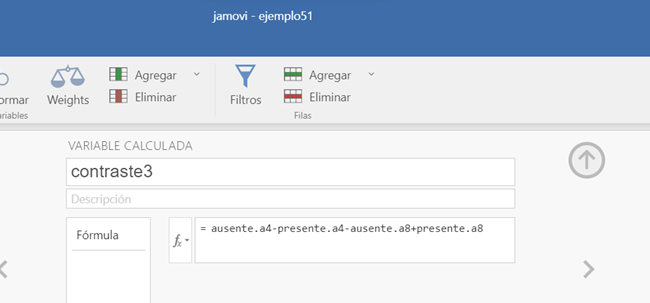
Figura 5.9: Modelo A2FMR en JAMOVI: Comparación de efectos simples

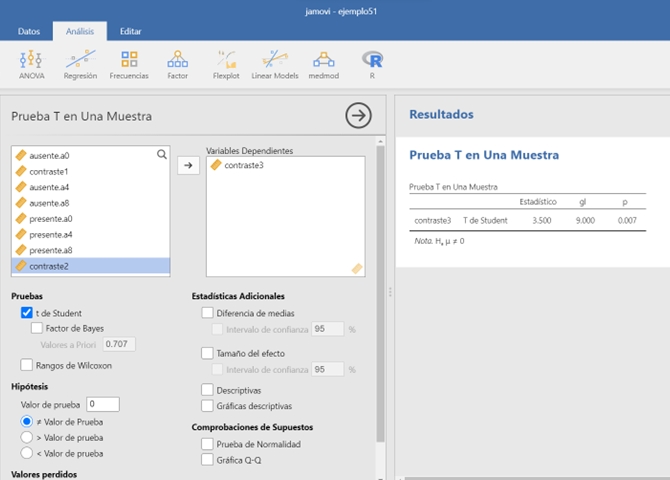
Figura 5.10: Modelo A2FMR en JAMOVI: Comparación de efectos simples

Estos resultados indican que también existen diferencias en la comparación de los efectos simples.

Conclusiones según normas APA: Se encontró la existencia de interacción entre las variables y el (F(2,18) = 45.31, p< .001, \(\eta_p^{2}\) = 0.67, indicando un TE grande). Se encontró que las diferencias en las medidas de presencia - ausencia con ángulo de 0 grados fueron menores cuando el ángulo fue de 4 grados (t(9)= 6.7, p < .001). También la diferencia ausencia - presencia fue mayor a los 8 grados que a los 0 (t(9)= 9.1, p < .001). Asimismo, el efecto de la presencia del ruido fue mayor a los 8 grados que a los 4 (t(9)= 3.5, p = .007).