6.5 Regresión múltiple y modelos estadísticos
Supongamos que estamos interesados en estudiar como influyen la edad y la educación en el tiempo de ejecución de la prueba TMT-B en el momento 1. Caben distintas hipótesis para entender las relaciones entre estas tres variables. La primera es considerar que el efecto de cada predictor es independiente. En este caso un modelo gráfico lo representaría de la siguiente forma:
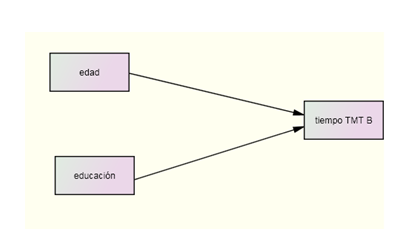
Figura 6.8: Modelo de regresión múltiple con relaciones directas
La representación estadística de este modelos sería la siguiente:
\[ Y_{i} = \beta_{0} + \beta_{1}*edad + \beta_{2}*educación + \epsilon_{i} \]
Sin embargo, con estas mismas tres variables es posible plantearse otras posibilidades de relación. Así, por ejemplo, podemos plantearnos que la relación entre la edad y el tiempo necesitado en completar la prueba del TMT-B está por la variable educación. En la siguiente figura aparece reflejado este modelo:
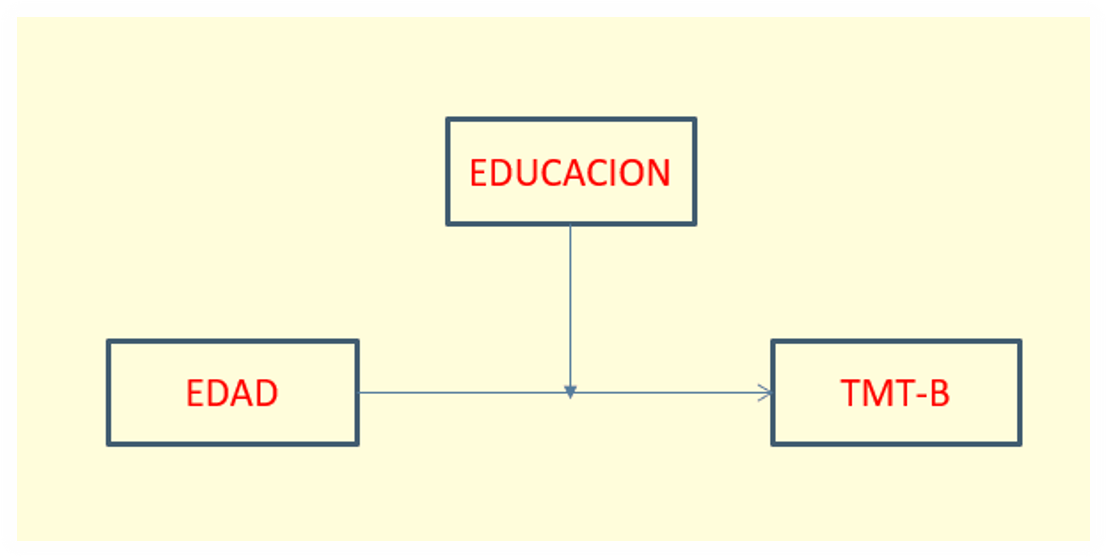
Figura 6.9: Modelo de moderación
El modelo estadístico que representa esta hipótesis es el siguiente:
\[ Y_{i} = \beta_{0} + \beta_{1}*edad + \beta_{2}*educación + \beta_{3}*educación*edad + \epsilon_{i} \]
Otra posibilidad sería considerar que la variable educación la relación entre la edad y la respuesta al TMT-B en la primera medición. Este modelo vendría representado de la siguiente forma:
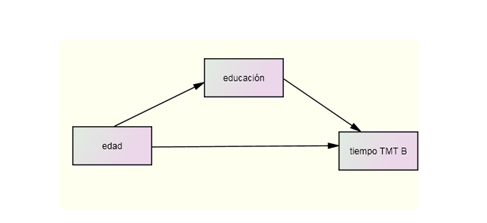
Figura 6.10: Modelo de mediación
Para contrastar este modelo son necesarias varias ecuaciones de regresión. En primer lugar, es necesario determinar la regresión de la variable mediadora (educación) sobre la variable predictora (edad):
\[ educación_{i} = \beta_{0} + \beta_{1}*edad + \epsilon_{i} \]
Asimismo, es necesario obtener la recta de regresión de la variable dependiente (TMTB) sobre la variable edad, estando presente la variable mediadora (educación):
\[ Y_{i} = \beta_{0} + \beta_{1}*edad + \beta_{2}*educación + \epsilon_{i} \]
A partir de estas dos regresiones puede determinarse los efectos mediadores de la variable educación.
Los conceptos de y así como los procedimientos estadísticos para determinarlos se estudiarán en los siguientes apartados.
6.5.0.1 Moderación con variables cualitativas
Consideremos que nos encontramos en una situación donde la variable actividades estimulantes (aec) es de naturaleza categórica (0 = baja estimulación y 1= alta estimulación), el modelo de regresión donde se quiere estudiar el efecto interactivo entre esta variable y la educación formal sería el siguiente:
\[ Atención_{i} = \beta_{0} + \beta_{1}*aec + \beta_{2}*educación + \beta_{2}*aec*educación + \epsilon_{i} \]
Los resultados obtenidos al aplicar este modelo son los siguientes:
En base a estos resultados podemos observar que existe una interacción significativa entre ambas variables. La ecuación de regresión para aquellos que tienen estimulación cognitiva alta (aec = 1) sería:
\[ Atención_{i} = 9.956 -28.389*1 + 13.052*educación + 9.874*educación*1 + \epsilon_{i} \]
Resolviendo:
\[ Atención_{i} = -18.433 + 22.926*educación + \epsilon_{i} \]
En el caso de las personas con baja estimulación cognitiva (aec = 0) la ecuación de regresión sería la siguiente:
\[ Atención_{i} = 9.956 -28.389*0 + 13.052*educación + 9.874*educación*0 + \epsilon_{i} \]
Simplificando:
\[ Atención_{i} = 9.956 + 13.052*educación + \epsilon_{i} \]

Figura 6.11: Relación entre la educación y la atención en función de las AEC
Gráficamente puede verse como la pendiente de la relación entre la educación formal y la atención es mayor cuando existe estimulación cognitiva alta que cuando la estimulación cognitiva es baja. O lo que es lo mismo: niveles altos y bajos de educación presentan mayores niveles de atención cuando la estimulación cognitiva es alta en comparación con los niveles bajos de estimulación cognitiva.
6.5.0.2 Moderación con variables cuantitativas
El procedimiento para interpretar la interacción en un modelo de regresión múltiple cuando todas las variables son cuantitativas es bastante parecido al caso en el que una variable predictora que participa en la interacción es cualitativa. Lo que se hace es dicotomizar la variable predictora cuantitativa. Por convenio, se suele considerar el valor de \(1.5\sigma\) como un valor alto en la variable predictora y \(-1.5\sigma\) como valor bajo de la variable. La única diferencia con el procedimiento anterior es que para evitar los problemas de colinealidad se recomienda centrar las variables (Cohen et al., 2003). Los resultados del análisis con las variables centradas aparecen a continuación:
Observamos que los niveles de colinealidad son tolerables y que el efecto de la interacción es significativo. Para poder interpretar esta interacción seleccionamos un valor alto de estimulación cognitiva (\(\mu\) +1.5\(\sigma\) = 34.7 +1.58.605 = 47.685) y un valor bajo de estimulación cognitiva (\(\mu\) -1.5\(\sigma\) = 8.09 -1.5.842 = 21.855).
Aplicando los valores de estimulación alta a la recta de regresión obtenida obtenemos los siguientes resultados:
\[ Atención_{i} = 174.124 +4.967*47.685 + 17.409*ceducación + .485*ceducación*47.685 + \epsilon_{i} \]
Simplificando:
\[ Atención_{i} = 410.975 + 40.536*ceducación + \epsilon_{i} \]
La ecuación para los individuos con niveles bajos de estimulación será:
\[ 174.124 +4.967*21.855 + 17.409*ceducación + .485*ceducación*21.855 + \epsilon_{i} \]
Agrupando los términos nos queda:
\[ Atención_{i} = 282.678 + 28*educación + \epsilon_{i} \]
Gráficamente podemos representar la interacción de la siguiente forma:

Figura 6.12: Relación entre la educación y la atención en función de las AEC
Mediante el gráfico puede interpretarse la interacción de la siguiente forma:
6.5.0.3 Modelo simple de mediación
Existe un modelo teórico que considera que el efecto de la edad sobre el deterioro cognitivo no es constante en todos los individuos. En algunos casos, las curvas de deterioro son muy pronunciadas, mientras que en otros el deterioro es menor e, incluso, plano (Salthouse et al., 2002). La interrelación entre estas variables puede estudiarse mediante los modelos de mediación y/o moderación. En este apartado nos centraremos en el estudio del modelo simple de mediación. Bajo esta hipótesis, las personas mayores que mantienen niveles altos de estimulación cognitiva podrían retrasar (compensar) el deterioro físico natural que se produce con el paso del tiempo. Es decir, mientras más estimulación cognitiva realizan las personas mayores, mayores conexiones sinápticas se producirán en el cerebro que compensarán la pérdida natural de neuronas. Por tanto, mientras más estimulación cognitiva tengamos mejor será nuestro funcionamiento cognitivo. Con este planteamiento estamos considerando que la estimulación cognitiva está mediando la relación existente entre la edad y el funcionamiento cognitivo. En la siguiente figura aparece el diagrama que representa este modelo:
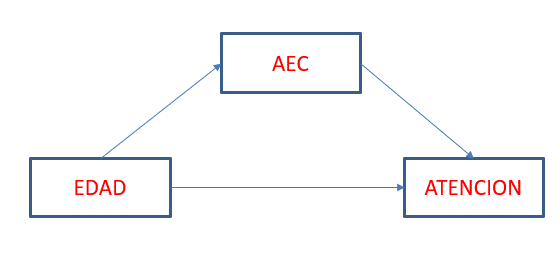
Figura 6.13: Modelo de mediación
Este modelo incluye dos variables dependientes ( y ) y dos variables predictoras ( y actividades estimulantes).
Bajo la hipótesis de la mediación simple se considera que el efecto de la edad se ve potenciado (o disminuido) por la realización de actividades estimulantes. El modelo asume una relación causal entre la variable edad sobre las actividades estimulantes y sobre la atención. Asimismo, en este modelo se considera también que existe una relación causal de la variable actividades estimulantes sobre la atención.
Para estudiar este modelo resulta necesario estimar tanto el efecto directo como el indirecto de la variable AEC. El es el coeficiente de regresión \(\beta_{1}\) de la recta de regresión Y (atención) sobre X (edad):
\[ Y_{i} = \beta_{0} + \beta_{1}*edad + \epsilon_{i} \]
Los resultados de esta ecuación de regresión son:
El cálculo del efecto indirecto se obtiene mediante el producto de dos coeficientes de regresión ( y ). El coeficiente es la pendiente de la recta de regresión de la variable mediadora (AEC) sobre la variable predictora (en nuestro caso la edad). Los resultados de esta recta de regresión se muestran a continuación:
El coeficiente se obtiene mediante la recta de regresión de la variable dependiente (atencion) sobre las predictoras (AEC y edad). El coeficiente es el valor de que multiplica a la variable mediadora. En nuestro ejemplo sería el siguiente:
El valor del coeficiente es de 7.898. Por tanto, el efecto indirecto será el producto de los coeficientes . El resultado será en nuestro caso (-0.503) \(\times\) 7.898 = -3.97. Este resultado representa el efecto indirecto en nuestra muestra. Para determinar el efecto indirecto a nivel poblacional tenemos que hacer una serie de suposiciones (distribución normal del efecto indirecto) que nos permite contrastarlo con la siguiente expresión:
\[ z = \frac{a \times b}{se_{ab}} \sim N(\mu,\sigma^{2}) \]
siendo \(se_{ab}\) el estimador del error estándar:
\[ se_{ab} = \sqrt{a^{2}se_{b}^2 + b^{2}se_{a}^{2}} \]
donde \(se_{b}\) es el error estándar del parámetro y \(se_{a}\) es el error estándar del parámetro a. En nuestro ejemplo, \(se_{a}\) = .192 y \(se_{b}\) = 1.979. Por tanto:
\[ se_{ab} = \sqrt{a^{2}se_{b}^2 + b^{2}se_{a}^{2}} = \sqrt{(-0.503)^2*2.086^2 +7.898^2* 0.199^2} = 1.89 \]
El valor del estadístico z es el siguiente: \[ z = \frac{-3.97} {1.89}= -2.10 > |1.96| \]
Observamos que existe un efecto indirecto significativo con un nivel de riesgo \(\alpha\) = 0.05 (\(p(z \pm 2.10)\) = .036).
Existen distintos programas que permiten realizar los cálculos del modelo de mediación simple. Por internet existen calculadoras como la siguiente:
https://datatab.es/statistics-calculator/moderator-mediator-analysis